Question

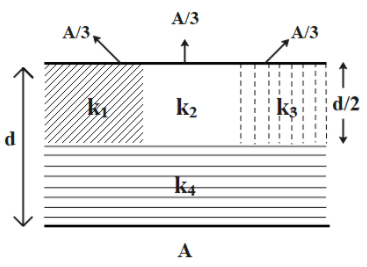
A parallel-plate capacitor of area A, plate separation and capacitance C is filled with four dielectric materials having dielectric constants ${k_1},{k_2},{k_3}{\text{ and }}{k_4}$ as shown in figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant $k$ is given by

A. $\dfrac{1}{k} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} + \dfrac{1}{{{k_3}}} + \dfrac{3}{{2{k_4}}}$
B. $k = {k_1} + {k_2} + {k_3} + 3{k_4}$
C. $k = \dfrac{2}{3}\left( {{k_1} + {k_2} + {k_3}} \right) + 2{k_4}$
D. $\dfrac{2}{k} = \dfrac{3}{{{k_1} + {k_2} + {k_3}}} + \dfrac{1}{{{k_4}}}$

Answer 1

Understand the structure of the given capacitor carefully and then divide it into a combination of its equivalent series or parallel connection of multiple capacitors. Then use the following mentioned formulas to get the required answer.

Formula Used:
Capacitance of a parallel plate capacitor,$C = \dfrac{{{\varepsilon _ \circ }A}}{d}$
Capacitance of a parallel plate capacitor with dielectric, $C = \dfrac{{k{\varepsilon _ \circ }A}}{d}$
In series connection, equivalent capacitance is:
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
In parallel connection, equivalent capacitance is:
$C = {C_1} + {C_2}$

Complete step by step answer:
A capacitor is a setup or arrangement of two conductors separated by an insulating medium that is used to store electric charge and electric energy. A capacitor usually consists of two conductors of any size and shape carrying different potentials and charges, and placed closed together in some definite positions relative to one another.
The capacitance of a capacitor is a constant that may be defined as the charge required to be supplied to either of the conductors of the capacitor so as to increase the potential difference between them by a unit amount. Its SI unit is the farad (F).
For a parallel plate capacitor, its capacitance is given as:
$C = \dfrac{{{\varepsilon _ \circ }A}}{d}$
The capacitance of a parallel capacitor when filled with a dielectric of dielectric constant k,
$C = \dfrac{{k{\varepsilon _ \circ }A}}{d} \cdots \cdots \cdots \cdots \cdots \left( 1 \right)$

Considering the given setup, we can divide it as two capacitors of capacitance ${C_1}{\text{ and }}{C_2}$ in series as shown below:

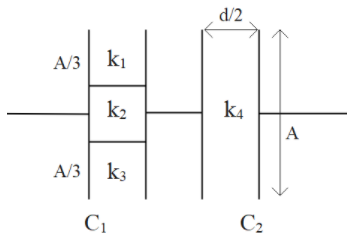
So the resultant capacitance of this setup will be C, which will be given by:
\eqalign{ & \dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} \cr & \Rightarrow \dfrac{d}{{A{\varepsilon _ \circ }k}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} \cr}
Now, the capacitor ${C_1}$has three capacitors inside it which are in parallel connection with each other. So their total capacitance can be calculated using the direct sum of capacitance of each capacitor.
\eqalign{ & \Rightarrow \dfrac{d}{{A{\varepsilon _ \circ }k}} = \dfrac{1}{{\dfrac{A}{3}{\varepsilon _ \circ }\dfrac{{\left( {{k_1} + {k_2} + {k_3}} \right)}}{{d/2}}}} + \dfrac{1}{{\dfrac{{A{\varepsilon _ \circ }{k_4}}}{{d/2}}}} \cr & \Rightarrow \dfrac{d}{k} = \dfrac{{3d}}{{2\left( {{k_1} + {k_2} + {k_3}} \right)}} + \dfrac{d}{{2{k_4}}} \cr & \therefore \dfrac{2}{k} = \dfrac{3}{{\left( {{k_1} + {k_2} + {k_3}} \right)}} + \dfrac{1}{{{k_4}}} \cr}
Therefore, the correct option is D. i.e., $\dfrac{2}{k} = \dfrac{3}{{{k_1} + {k_2} + {k_3}}} + \dfrac{1}{{{k_4}}}$

Note: In series connection of capacitors, each capacitor has an equal amount of charge for any value of given capacitance. On the other hand in parallel connection of capacitors, the potential differences of the capacitors connected in parallel are equal for any value of capacitances.