Question

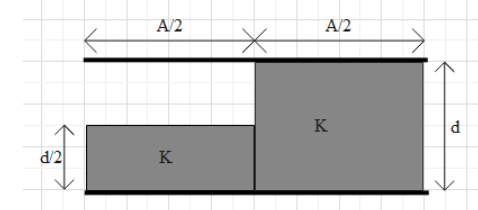
A parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangements?

$\text{A}\text{. }\dfrac{3K{{\varepsilon }_{0}}A}{4d}$
$\text{B}\text{. }\dfrac{4K{{\varepsilon }_{0}}A}{3d}$
$\text{C}\text{. }\dfrac{(K+1){{\varepsilon }_{0}}A}{2d}$
$\text{D}\text{. }\dfrac{K(K+3){{\varepsilon }_{0}}A}{2(K+1)d}$

Answer 1

When a dielectric medium (material) is inserted in between the parallel plates of a capacitance, the capacitor acts as a new capacitor with more capacitance value. i.e. $C'=\dfrac{k{{\varepsilon }_{{}^\circ }}A}{d}=kC$. If there are more than one dielectric materials, each dielectric material acts as a separate capacitor. Then we can convert the dielectrics into capacitors, which makes the work easier. Also, use the formulas for finding the equivalent capacitance when the capacitors are in series and parallel connection.

Formula Used :
$C'=\dfrac{k{{\varepsilon }_{{}^\circ }}A}{d}=kC$
$\Rightarrow \dfrac{1}{{{C}_{12}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$
${{C}_{123}}={{C}_{12}}+{{C}_{3}}$

Complete step-by-step answer :
The capacitance of capacitor is given as $C=\dfrac{{{\varepsilon }_{\circ }}A}{d}$ , where C is the capacitance of the capacitor, A is area of parallel metal plates, d is the perpendicular distance between the two parallel plates and ${{\varepsilon }_{\circ }}$ is the permittivity of the free space. This value of capacitance is when there is air in the space between the plates. If there is another medium, which we call as dielectric then the capacitance of the capacitor changes. Dielectric medium is a poor conducting material that creates an internal electric field when an external electric field acts on it.
To understand the new electric field created between the plates after adding the dielectric material, we have something known as dielectric constant (k). $k=\dfrac{E}{E'}$, where E is the electric field without the dielectric material and E’ is the reduced electric field after inserting the dielectric material. The value of k is always greater than one.
When a dielectric material is inserted in between the parallel plates of the capacitor, the capacitance of the capacitor increases by a factor of K called dielectric constant. Therefore, the new capacitance becomes $C'=\dfrac{k{{\varepsilon }_{\circ }}A}{d}=kC$.
So the dielectric acts as an updated capacitor in the circuit.
Air is also a dielectric medium with dielectric constant equal to 1.
In the given figure, there are three dielectrics. Let the dielectrics be ${{k}_{1}}$, ${{k}_{2}}$ and ${{k}_{3}}$ as shown in the figure below.

If you see the given figure, we can divide it into three different capacitors. Let the capacitance with dielectric constants ${{k}_{1}}$, ${{k}_{2}}$ and ${{k}_{3}}$ be ${{C}_{1}}$, ${{C}_{2}}$ and ${{C}_{3}}$ respectively. Let us now write the expression for each capacitance.
The width of the capacitor (${{C}_{1}}$) is $\dfrac{d}{2}$ and the area is $\dfrac{A}{2}$, so the capacitance ${{C}_{1}}={{k}_{1}}\dfrac{{{\varepsilon }_{\circ }}\left( \dfrac{A}{2} \right)}{\left( \dfrac{d}{2} \right)}={{k}_{1}}\dfrac{{{\varepsilon }_{\circ }}A}{d}$.
Here ${{k}_{1}}=1$
Therefore, ${{C}_{1}}=\dfrac{{{\varepsilon }_{\circ }}A}{d}$ ……….(1)
Similarly, the capacitance${{C}_{2}}={{k}_{2}}\dfrac{{{\varepsilon }_{\circ }}\left( \dfrac{A}{2} \right)}{\left( \dfrac{d}{2} \right)}={{k}_{2}}\dfrac{{{\varepsilon }_{\circ }}A}{d}$.
And ${{k}_{2}}=k$
Therefore, ${{C}_{2}}=k\dfrac{{{\varepsilon }_{\circ }}A}{d}$ ……..(2).
The width of the third capacitor (${{C}_{3}}$) is d and the area is $\dfrac{A}{2}$. Therefore, the capacitance${{C}_{3}}={{k}_{3}}\dfrac{{{\varepsilon }_{\circ }}\dfrac{A}{2}}{d}={{k}_{3}}\dfrac{{{\varepsilon }_{\circ }}A}{2d}$ ……….(3).
And ${{k}_{3}}=k$
Therefore, ${{C}_{3}}=k\dfrac{{{\varepsilon }_{\circ }}A}{2d}$.
As we can see that the dielectric with electric constants ${{k}_{1}}$ and ${{k}_{2}}$ are in series and ${{k}_{3}}$ is in parallel with the series connection of ${{k}_{1}}$ and ${{k}_{3}}$. Redraw the figure and replace the dielectrics with their respective capacitance as shown. It will be easier to understand.

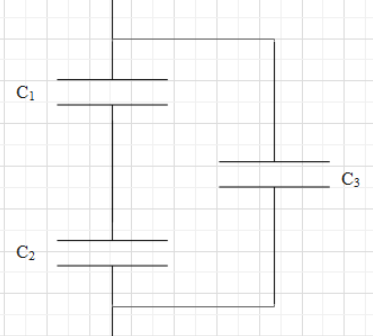
The capacitors ${{C}_{1}}$ and ${{C}_{2}}$ are in series. So reciprocal of the effective capacitance (${{C}_{12}}$) of these two will be the sum of the reciprocals of the two capacitances.
$\Rightarrow \dfrac{1}{{{C}_{12}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$. Substitute the values of ${{C}_{1}}$ and ${{C}_{2}}$ from equations (1) and (2).
Therefore, $\dfrac{1}{{{C}_{12}}}=\dfrac{1}{\dfrac{{{\varepsilon }_{\circ }}A}{d}}+\dfrac{1}{k\dfrac{{{\varepsilon }_{\circ }}A}{d}}=\left( 1+\dfrac{1}{k} \right)\dfrac{1}{\dfrac{{{\varepsilon }_{\circ }}A}{d}}$.
$\Rightarrow {{C}_{12}}=\dfrac{k}{\left( 1+k \right)}\dfrac{{{\varepsilon }_{\circ }}A}{d}$…….(4)
The capacitor ${{C}_{3}}$ is in parallel with ${{C}_{12}}$. The effective capacitance (${{C}_{123}}$) of these two will be the sum of the individual capacitance i.e.
${{C}_{123}}={{C}_{12}}+{{C}_{3}}$ .
Substitute the values of ${{C}_{12}}$ and ${{C}_{3}}$ from equations (3) and (4).
${{C}_{123}}=\dfrac{k}{\left( 1+k \right)}\dfrac{{{\varepsilon }_{\circ }}A}{d}+k\dfrac{{{\varepsilon }_{\circ }}A}{2d}$
$\Rightarrow {{C}_{123}}=\left[ \dfrac{1}{\left( 1+k \right)}+\dfrac{1}{2} \right]\dfrac{k{{\varepsilon }_{\circ }}A}{d}$
$\Rightarrow {{C}_{123}}=\left[ \dfrac{2+1+k}{2\left( 1+k \right)} \right]\dfrac{k{{\varepsilon }_{\circ }}A}{d}$
Therefore, ${{C}_{123}}=\dfrac{k(k+3){{\varepsilon }_{\circ }}A}{2(k+1)d}$ ……..(5)
Hence, the correct option is (D).

Note :Different materials have different values of dielectric constant. The perfectly conducting materials have the value dielectric constants as infinity ($k=\infty$). A perfectly insulating material has the value of dielectric constant as zero ($k=0$).
In these types of questions, always remember to convert the dielectrics into capacitors. Then check which are in series and which are in parallel connection and solve accordingly.