Question
Question: A parallel plate capacitor is made of two square plates of side ‘a’, separated by a distance d(d << ...
A parallel plate capacitor is made of two square plates of side ‘a’, separated by a distance d(d << a). The lower triangular portion is filled with a dielectric of dielectric constant K. Find the capacitance of the capacitor.
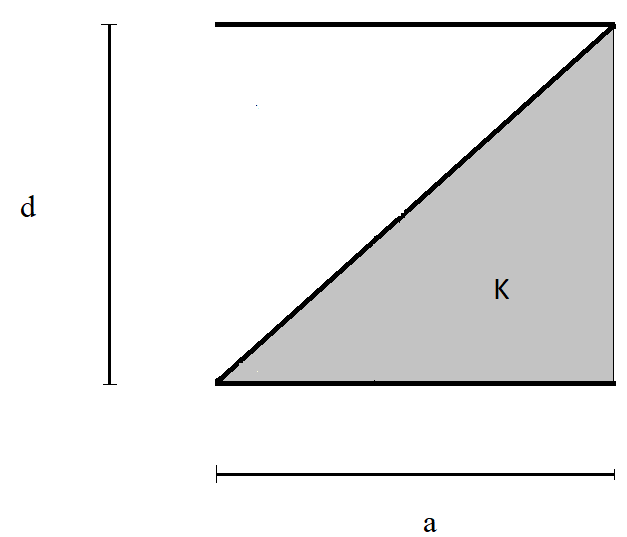
Solution
Integrating cross-sectional areas using elemental parameters will reveal the whole area with actual parameters. Integration of capacitance of a cross-sectional area of a parallel plate capacitor over the whole area will help to determine the total capacitance of the parallel plate capacitor.
Formula used: For a parallel plate capacitor,
C=dK ε0a
Here,
K is the relative permittivity of the dielectric medium
ε0 is the permittivity of free space
a is the area of the plates
d is the distance between the plates
Complete step by step answer:
In this tricky question, it is important to approach by taking a small cross-sectional area of the parallel plate capacitor. We need to find the capacitance of the cross-sectional area first. Then, we integrate the calculated capacitance over the whole area to determine the total capacitance of the parallel plate capacitor. The figure given below will give a clear picture of the whole idea.
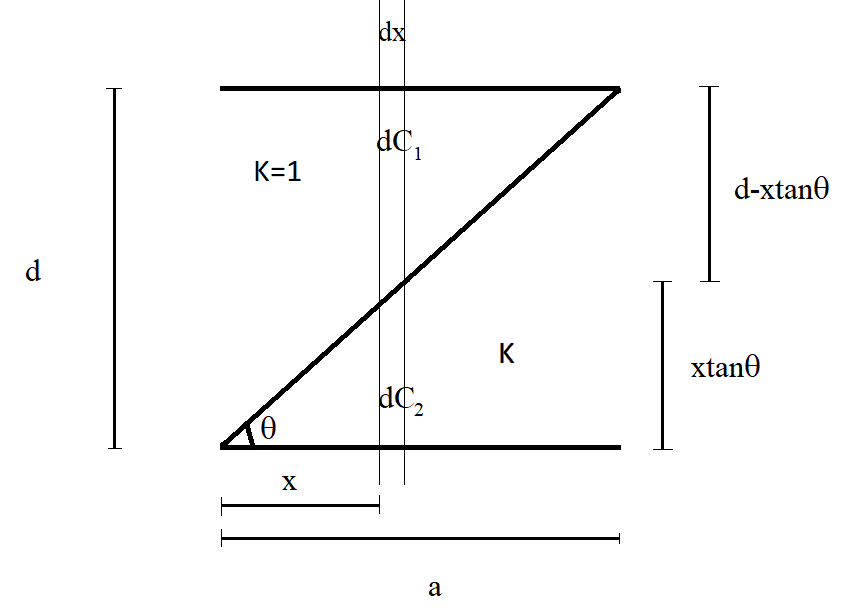
From the figure, it can be understood that the two plates of the parallel plate capacitor are separated by a distance d and that the area of each plate is a. The upper half triangle is free space with K=1 and the lower half triangle is filled with a dielectric of dielectric constant K. We have taken a small cross-sectional area at a distance x from one of the ends of the capacitor. Let one of the angles of the lower half triangle with the dielectric be θ. The length of the cross-sectional area is dx and the elemental area of the same is adx. The cross-sectional area of the parallel plate capacitor can be considered as two capacitors dC1 and dC2 connected in series. It is clear from the figure that dC1 is present in the region where K=1 and dC2 is present in the region where K=K. It is also clear that the length of dC1 is equal to d−xtanθ and the length of dC2 is xtanθ. Now, we have to find the total capacitance of the cross-sectional area of the capacitor. Let us call this capacitance dC. Both the capacitors dC1 and dC2 are connected in series. When capacitors are joined in series, we have the relation: dC1=dC11+dC21
Applying the formula for capacitance to both dC1 and dC2, we have:
dC1=d−xtanθ ε0(adx)
dC2=xtanθKε0(adx)
Substituting these values in the above equation, we have:
