Question
Question: A parallel plate capacitor is made of two plates of length l, width w and separated by distance d. A...
A parallel plate capacitor is made of two plates of length l, width w and separated by distance d. A dielectric slab (dielectric constant K) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force F=−dxdU where U is the energy of the capacitor when dielectric is inside the capacitor up to distance x (See figure). If the charge on the capacitor is Q then the force on the dielectric when it is near the edge is
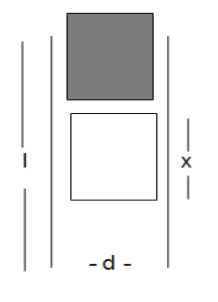
Solution
Here, we will use the relation between the capacitance of a capacitor, dielectric constant and area. This will give us net capacitance. This will further be used to find potential and then finally the force on the dielectric when it is near the edge. We will also discuss some basics of capacitor and dielectric constant.
Formula used
C=dKε0A
U=2C′Q2
F=−dxdU
Complete answer:
To get the required force on dielectric, let at any moment of time when the slab travelled distance x then the capacitance due to the dielectric slab is:
\eqalign{
& {C_d} = \dfrac{{K{\varepsilon _0}A}}{d} \cr
& {C_d} = \dfrac{{K{\varepsilon _0}(wx)}}{d} \cr}
Capacitance where the slab is not present is given by:
C=dε0(w(1−x))
So, net capacitance will be given as:
C′=dwε0(1+(k−1)x)
Now, energy U is given as:
\eqalign{
& U = \dfrac{{{Q^2}}}{{2C'}} \cr
& \Rightarrow U = \dfrac{{{Q^2}d}}{{2w{\varepsilon _0}1}}\left( {\dfrac{1}{{1 + \dfrac{{(K - 1)x}}{1}}}} \right) \cr
& \because F = \dfrac{{ - dU}}{{dx}} \cr
& \therefore F = \dfrac{{{Q^2}d}}{{2w{\varepsilon _0}1}}(K - 1) \cr}
Therefore, we get the required value of force on the dielectric, when it is near the edge is given by F.
Additional information:
A capacitor consists of two or more parallel conductive or metal plates. These plates are not connected or touching each other, but rather they are electrically separated either by air or by some form of a good insulating material like waxed paper, mica, ceramic, plastic or some form of a liquid gel as used in electrolytic capacitors. This insulating layer between capacitor’s plates is commonly called the Dielectric.
The dielectric constant is defined as a measure of the amount of electric potential energy, in the form of induced polarization which is stored in a given volume of material under the action of an electric field.
Note:
Capacitance is measured in Farad, or can be said as one coulomb per volt. Capacitance is dependent on the dielectric constant as well as on the distance between the two plates. The parallel plate capacitor is the simplest form of capacitor.
