Question

A parallel plate capacitor is charged by a battery, which is then disconnected. A dielectric slab is then inserted in the space between the plates. Explain what changes, if any, occur in the values of
(A). capacitance
(B). potential difference between the plates
(C). Electric field between the plates
(D). Energy stored in the capacitor

Answer 1

The dielectric slab acts as an insulator and polarization of charges occur within it due to which capacitor’s properties like electric field, capacitance, potential difference get affected. The polarization in the dielectric is opposite to the polarization on the plates. The dielectric changes the medium inside the capacitor and hence the permeability.

Formulas Used:
$V=E\times d$
$C=\dfrac{q}{V}$
$E=\dfrac{1}{2}C{{V}^{2}}$

Complete step by step solution:
The capacitance is the ability of a conductor to store charge inside it. Its SI unit is farad ($F$).
A dielectric slab is an insulating material in which polarization of charges occur. When it is introduced between the plates of a capacitor, the positive charges are attracted to the plates containing negative charges and the negative charges are attracted towards the positively charged plate due to which polarization in the dielectric is opposite to the polarity of plates of parallel plate capacitor.
An electric field with direction opposite to the field of capacitor develops in the dielectric and it cancels the electric field of the capacitor. Therefore, the electric field decreases.

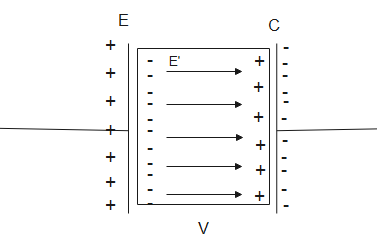
As we know that,
$V=E\times d$
Here, $V$ is the potential difference between the plates of capacitor
$d$ is length of the space between the plates of capacitor
$E$ is the electric field.
Therefore,
$V\propto E$
From the above relation as $E$ decreases,$V$ also decreases.
We know, the capacitance is given by-
$C=\dfrac{q}{V}$
Therefore,$C\propto \dfrac{1}{V}$
From the above relation, as $V$ decreases capacitance increases.
The formula for energy stored in a capacitor is-
$E=\dfrac{1}{2}C{{V}^{2}}$
It can also be written as-
$E=\dfrac{1}{2}\dfrac{{{q}^{2}}}{C}$
As the capacitance increases, the energy stored in it decreases.

Therefore, with the introduction of a dielectric slab in a capacitor-
(A). Capacitance increases
(B). Potential difference between the plates decreases
(C). Electric field between the plates decreases
(D). Energy stored in the capacitor decreases.

Note:
The introduction of a dielectric slab between the plates of the capacitor changes the permeability of the space between the plates. A combination of dielectric arranged in series or parallel can also be introduced. If we insert a metal plate between the capacitor, it acts as an infinite storage of charge, which means it gets short-circuited. The introduction of dielectric does not affect the charge stored, charge remains constant.