Question
Question: A parallel plate capacitor having plates of area S and plate separation d, has capacitance \(C_1\) ...
A parallel plate capacitor having plates of area S and plate separation d, has capacitance C1 in air. When two dielectrics of different relative permittivity (ε1=2,ε2=4) are introduced between the two plates as shown in the figure, the capacitance become C2. The ratio C1C2 is.
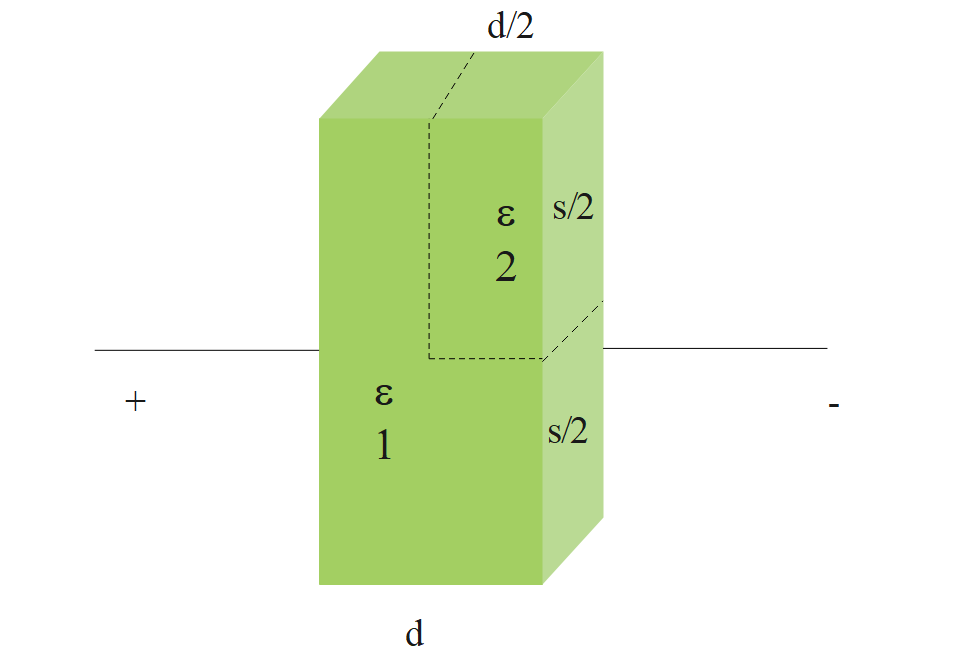
Solution
Let us first divide the capacitor into three parts. The first part is the top part beside the new dielectric. The second is the part of the capacitor that is now introduced with new permittivity. The third part is the bottom part of the whole capacitor. We need to find the equivalent capacitor of the new capacitor formed by introducing new permittivity and divide it with the old net capacitance.
Formula used:
C=dεA
Complete step by step answer:
let us first wire down the given quantities and values,
Area of the capacitor is S
Plate separation is d.
Let us first find the capacitance of the capacitor when it is in the air,
C1=dεAC1=dεS
Now, let us find the capacitance of the capacitor when dielectrics are inserted,
Let u divide the three parts into C2,C3,C4
C2will be the capacitance of the part where dielectric is inserted,
C2=dε2S⇒C2=d4ε0S
C3will be the capacitance of the part adjacent to C2
C3=dε1S⇒C3=d2ε0S
The third part is the capacitance of the rest capacitor,
C4=dε0S
Now, the effective resistance of the two parts that are adjacent will be,
As they are in series,
Ceff=C1+C2C1×C2⇒Ceff=d6ε0Sd4ε0S×d2ε0S⇒Ceff=3d4ε0S
Now, the remaining part of the capacitor and this effective capacitance are in parallel, the net capacitance now will be,
Ceq=d4ε0S+dε0S⇒Ceq=d7ε0S
The ratio between the effective capacitance that we obtained now and the initial capacitance will be,
ratio=dε0Sd7ε0S∴ratio=37
Note: The effective combination of the capacitors and resistances are a lot different. They are opposite to each other. The equivalent resistance of two resistor formulas will be the same as the series combination of the capacitors, they are quite opposite. The same goes for the series resistance and parallel capacitors. So, we need to be sure during the calculations of series and [parallel combinations of capacitors and resistors.
