Question

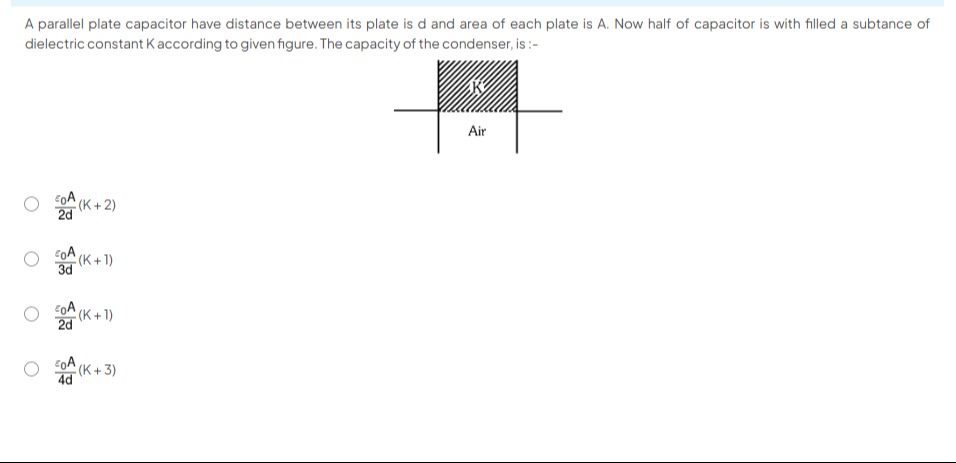
A parallel plate capacitor have distance between its plate is d and area of each plate is A. Now half of capacitor is with filled a subtance of dielectric constant K according to given figure. The capacity of the condenser, is :-

• A. $\frac{\epsilon_0 A}{2d}(K+2)$
• B. $\frac{\epsilon_0 A}{3d}(K+1)$
• C. $\frac{\epsilon_0 A}{2d}(K+1)$
• D. $\frac{\epsilon_0 A}{4d}(K+3)$

Answer 1

Answer: (C)

$\frac{\epsilon_0 A}{2d}(K+1)$

Answer 2

The problem describes a parallel plate capacitor with plate area A and plate separation d. Half of the capacitor is filled with a dielectric material of dielectric constant K, and the other half is filled with air (dielectric constant $K_{air} = 1$). The figure indicates that the dielectric material and air fill the capacitor such that they divide the area of the plates, while maintaining the full distance d between the plates for both sections.

This configuration can be viewed as two capacitors connected in parallel.

Capacitor 1 (with dielectric K):

• Area of plates, $A_1 = A/2$
• Distance between plates, $d_1 = d$
• Dielectric constant, $K_1 = K$

The capacitance of this part is given by: $C_1 = \frac{K_1 \epsilon_0 A_1}{d_1} = \frac{K \epsilon_0 (A/2)}{d} = \frac{K \epsilon_0 A}{2d}$

Capacitor 2 (with air):

• Area of plates, $A_2 = A/2$
• Distance between plates, $d_2 = d$
• Dielectric constant, $K_2 = 1$ (for air)

The capacitance of this part is given by: $C_2 = \frac{K_2 \epsilon_0 A_2}{d_2} = \frac{1 \cdot \epsilon_0 (A/2)}{d} = \frac{\epsilon_0 A}{2d}$

Since these two capacitors are connected in parallel (they share the same potential difference across their plates), the total equivalent capacitance ($C_{eq}$) is the sum of their individual capacitances: $C_{eq} = C_1 + C_2$ $C_{eq} = \frac{K \epsilon_0 A}{2d} + \frac{\epsilon_0 A}{2d}$ $C_{eq} = \frac{\epsilon_0 A}{2d} (K + 1)$