Question
Question: A parallel plate capacitor has two layers of dielectric as shown in figure. If this capacitor is con...
A parallel plate capacitor has two layers of dielectric as shown in figure. If this capacitor is connected across a battery, then the ratio of potential difference across the dielectric layer is
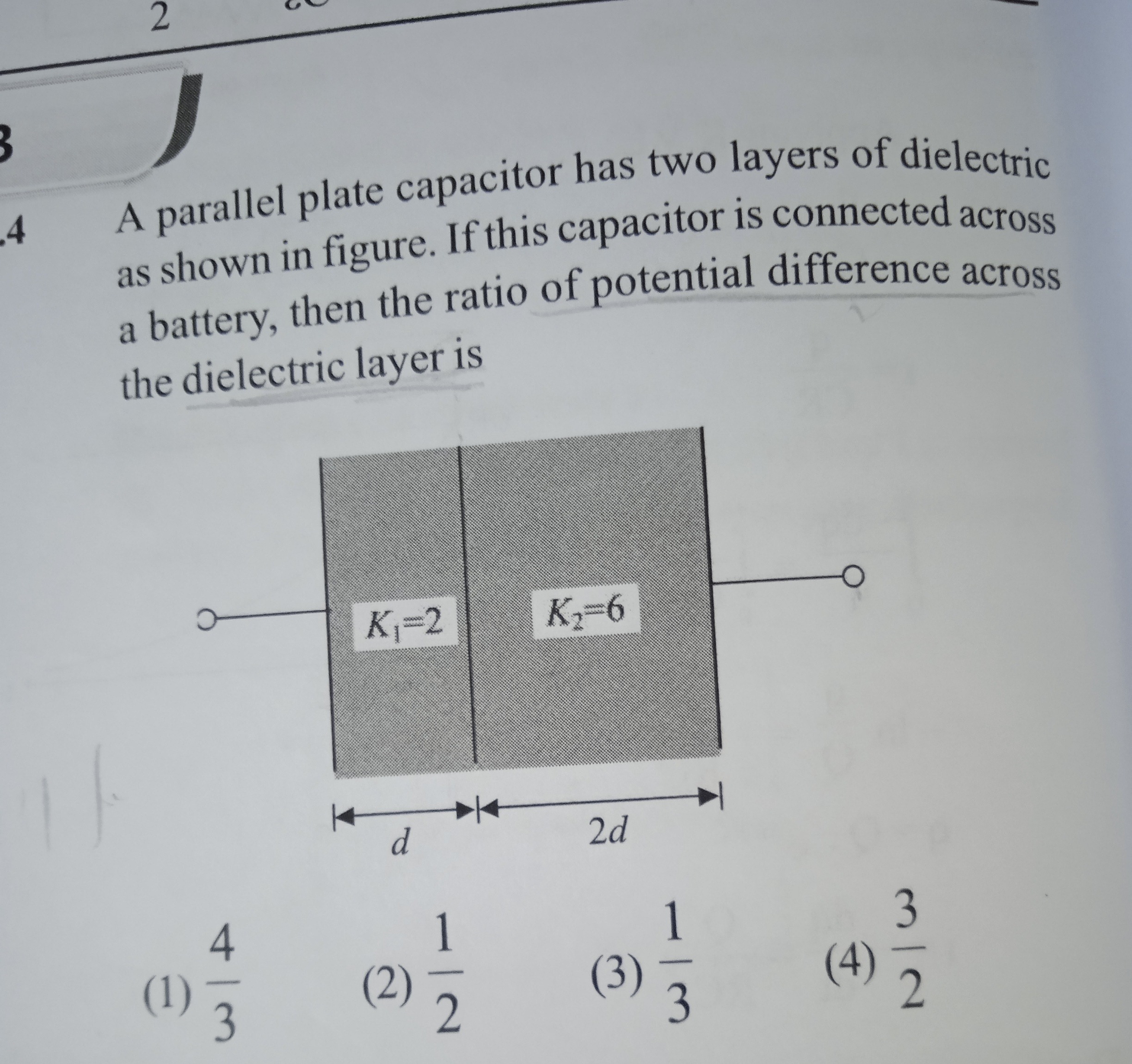
34
21
31
23
3/2
Solution
The given setup shows a parallel plate capacitor with two dielectric layers placed side-by-side, effectively forming two capacitors in series.
-
Identify the components:
- Layer 1: Dielectric constant K1=2, thickness d1=d.
- Layer 2: Dielectric constant K2=6, thickness d2=2d. Let the area of the capacitor plates be A.
-
Capacitance of each layer: The capacitance of a parallel plate capacitor with a dielectric of constant K and thickness t is given by C=tKϵ0A.
- Capacitance of the first layer (C1): C1=d1K1ϵ0A=d2ϵ0A
- Capacitance of the second layer (C2): C2=d2K2ϵ0A=2d6ϵ0A=d3ϵ0A
-
Potential difference across layers: Since the two dielectric layers are in series, the charge (Q) stored on each equivalent capacitor is the same. The potential difference across a capacitor is given by V=CQ.
- Potential difference across the first layer (V1): V1=C1Q=d2ϵ0AQ=2ϵ0AQd
- Potential difference across the second layer (V2): V2=C2Q=d3ϵ0AQ=3ϵ0AQd
-
Ratio of potential differences: The ratio of potential difference across the dielectric layers is V2V1: V2V1=3ϵ0AQd2ϵ0AQd V2V1=2ϵ0AQd×Qd3ϵ0A V2V1=23
The ratio of potential difference across the dielectric layers is 23.
