Question

A parallel plate capacitor has capacitance of $1\mu F$. Both the plates are given a charge of $2\mu C,4\mu C$. The potential difference developed across the capacitor is:
$\begin{aligned} & a)5V \\\ & b)2V \\\ & c)3V \\\ & d)1V \\\ \end{aligned}$

Answer 1

We can find the electric field on both the plates. Next, find out the net electric field on the capacitor. Find the voltage across the circuit as voltage can be expressed in terms of capacitance, which is given an electric field, which can be found out.

Formula used:
$\begin{aligned} & E=\dfrac{\sigma }{2{{\varepsilon }_{0}}} \\\ & \sigma =\dfrac{Q}{A} \\\ & C=\dfrac{{{\varepsilon }_{0}}A}{d} \\\ & V=Ed \\\ \end{aligned}$

Complete step-by-step solution:
__
Given, the charges on the plates are ${{Q}_{1}},{{Q}_{2}}={{q}_{1}},{{q}_{2}}=4\mu C,2\mu C$.the electric field due to the charges on the plates is,
$E=\dfrac{Q}{2A{{\varepsilon }_{0}}}$
Therefore, the net electric field due to both the charges is,
${{E}_{net}}=\dfrac{4}{2A{{\varepsilon }_{0}}}-\dfrac{2}{2A{{\varepsilon }_{0}}}=\dfrac{1}{A{{\varepsilon }_{0}}}$
Now, we know,
$\begin{aligned} & V=Ed \\\ & V=\dfrac{1}{A{{\varepsilon }_{0}}}d \\\ & V=\dfrac{1}{C} \\\ \end{aligned}$
Given, capacitance of the circuit as $1\mu F$
Therefore, the voltage across the circuit will be,
$\begin{aligned} & V=\dfrac{1}{C} \\\ & V=1V \\\ \end{aligned}$
Therefore, the correct option is option d.

Additional information:
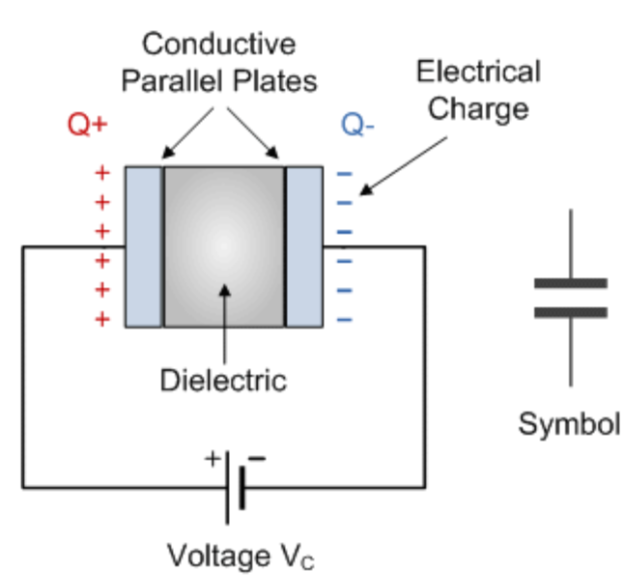
A capacitor is a component, which has the ability or capacity to store energy as an electric charge producing a potential difference or generating some amount of voltage across the plates. A capacitor consists of two or more parallel conducting metal plates, which are not connected or touching each other but are separated by air or another dielectric material. The conductive plates in the capacitor are usually round, square, or rectangular in shape. When an external voltage is supplied, the current flows without negligible resistance or no resistance at all. If the flow of electrons is occurring in between the plates, the current is known as charging current. The strength or rate if this charging current is maximum when plates are discharged fully and slowly reduces its value to zero when they are fully charged.

Note: If the charges present on the plates are not of the same sign, the net electric field acting on the plates might change accordingly. In the above question, both the charges on the capacitor plates are positive. All the units of the values must be of the same system. If not, make the changes to the SI unit or any other unit system.