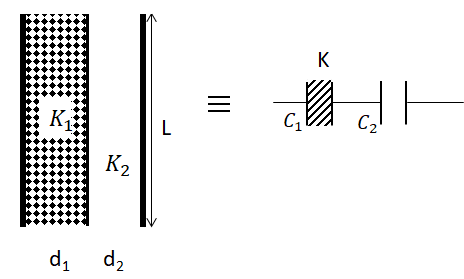Question
Question: A parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that co...
A parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 31 of the area of its plates, as shown in the figure. The total capacitance is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charged Q1 and the rest of the area gets charged Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring the edge effects:
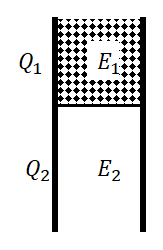
A. E2E1=1B. E2E1=K1C. Q2Q1=K3D. C1C=K2+K
Solution
Hint: The capacitance of a parallel plate capacitor needs to be found in this problem. The formula of a parallel plate capacitor is given by: C=dK∈0A. For capacitors in parallel to each other, the net capacitance is given by, Cnet=C1+C2. Further, for parallel plate capacitor, the charge of the capacitor is given by, Q=CVand the Electric field of the parallel plate capacitor is given by E=Vd.
Step by step solution:
Let’s make a more detailed diagram of the problem given.
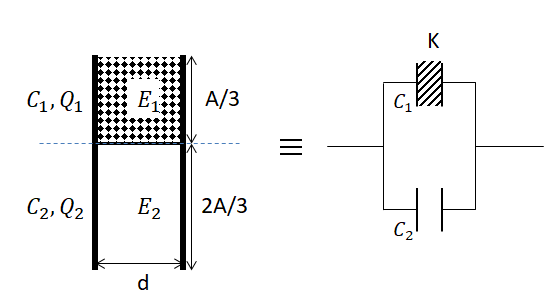
From the problem, we are given that the slab of dielectric constant (K) in between the plates, covers an area of 3A. The rest of the capacitor is filled with air having dielectric constant (K=1). The division of this parallel plate capacitor makes it similar to two capacitors of capacitance (C1)and (C2) which are parallel to each other. Therefore the net capacitance of this parallel plate capacitor (C) is given by: C=C1+C2.
The capacitance of a parallel plate capacitor of dielectric constant (K) and area in between the parallel plate capacitor (A) and the distance between the plates of the capacitor (d) is: C=dK∈0A.
Therefore, the capacitance (C1)is: C1=dK∈0(3A)⇒C1=3dK∈0A.
Similarly, the capacitance (C2) is: C2=dK∈0(32A)⇒C2=3d(1)∈0(2A)⇒C2=3d2∈0A.
Therefore the ratio of these capacitance become: C2C1=3d2∈0A3dK∈0A=2K⇒C1C2=K2.
Adding (1) on both sides of the above equation makes it: C1C2+1=K2+1⇒C1C2+C1C1=K2+KK⇒C1C1+C2=K2+K⇒C1C=K2+K.
Therefore, the ratio of the capacitance of the whole capacitor, to the capacitance of part containing the dielectric slab (K) is: C1C=K2+K.
We also know that the amount of charge in a parallel plate capacitor is givenQ=CV. In the current case, the capacitances of (C1)and (C2) are both a part of the common capacitor (C). Hence, the potential (V) remains constant. Therefore: Q∝C. This implies: Q2Q1=C2C1=2K⇒Q2Q1=2K.
The Electric field of a parallel plate capacitor is given by, E=Vd. For the current case, the potential remains constant, as the capacitances (C1)and (C2) are both a part of the common capacitor (C). Therefore: E∝d. For this case, the distance between the plates is constant. Hence, E2E1=dd=1⇒E2E1=1.
Therefore, the options A and D, are the solutions.
Note:
In this problem, when different dielectrics are kept in a parallel plate capacitor, horizontally one below the other, it is similar to two parallel plates capacitors being parallel to each other as in the image below.
Similarly, if there are two different dielectrics encased in a parallel plate capacitor vertically, one beside another, then it will be similar to two dielectrics in series with each other as in the image below.