Question

A parallel plate capacitor has a capacitance C. when it is half-filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
A) 400%
B) 66.66%
C) 33.3%
D) 200%

Answer 1

Use the equation of a parallel plate capacitor with a dielectric slab and calculate the increase in the capacitance of the capacitor.

Complete step by step solution:
Figure 1: depicts the situation mentioned above

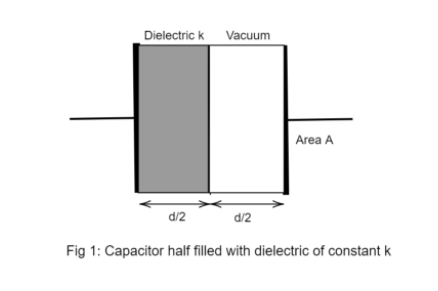
Step1:
Use the equation of capacitance of a parallel plate capacitor, so the initial capacitance was,
$C = \dfrac{{{ \in _ \circ }A}}{d}$ …….(1)
Now when we filled the capacitance half with a dielectric and capacitance,
${C_1} = \dfrac{{k{ \in _ \circ }A}}{{\dfrac{d}{2}}} \\\ \Rightarrow {C_1} = \dfrac{{2k{ \in _ \circ }A}}{d} \\\$
Where k is the dielectric constant.
Now calculate the capacitance of rest half of the capacitor,

$${C_2} = \dfrac{{{ \in _ \circ }A}}{{\dfrac{d}{2}}} \\\ \Rightarrow {C_2} = \dfrac{{2{ \in _ \circ }A}}{d} \\\$$

Step2:
Now these capacitors ${C_1}$and ${C_2}$are in parallel connection,
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
Substitute the values in the above equation and calculate the new total capacitance-
$\dfrac{1}{C} = \dfrac{d}{{2{ \in _ \circ }A}}\left( {\dfrac{1}{k} + 1} \right)$
On substituting the corresponding values, we get
$\Rightarrow \dfrac{1}{C} = \dfrac{d}{{2{ \in _ \circ }A}}\left( {\dfrac{1}{5} + 1} \right)$
On simplification of the above equation,
$\Rightarrow \dfrac{1}{C} = \left( {\dfrac{6}{5}} \right)\dfrac{d}{{2{ \in _ \circ }A}}$
On further simplification, we get
$\Rightarrow \dfrac{1}{C} = \dfrac{3}{5}\dfrac{d}{{{ \in _ \circ }A}}$
$\Rightarrow C = \dfrac{5}{3}\dfrac{{{ \in _ \circ }A}}{d}$
Step3:
Now calculate the percentage increase in capacitance,
% age increase in capacitance,
$\Rightarrow \dfrac{{\dfrac{5}{3}\dfrac{{{ \in _ \circ }A}}{d} - \dfrac{{{ \in _ \circ }A}}{d}}}{{\dfrac{{{ \in _ \circ }A}}{d}}} \times 100$
On simplification,
$= \dfrac{2}{3} \times 100$
$= 66.66\%$

$\therefore$ The percentage increase in the capacitance will be $66.66\%$. Hence, option (B) is the correct answer.

Additional Information:
Capacitors considered being voltage stabilizers in AC circuits across the load. It doesn’t allow DC current to pass through it. Hence, It acts as a voltage barrier for DC. But in the case of AC circuits when there is a change in voltage from the source then because of stored charge or charged capacitor across load we get supply from capacitor to sudden drop compensation. Therefore, it is necessary to increase capacitance to sustain heavier loads by adding dielectric materials into it.

Note:
Keep in mind that capacitance always increases with the introduction of a dielectric slab. The percentage increase in capacitance always calculated over the initial original capacitance.
Do remember the equation of capacitance of a parallel plate capacitor:
$C = \dfrac{{{ \in _ \circ }A}}{d}$