Question

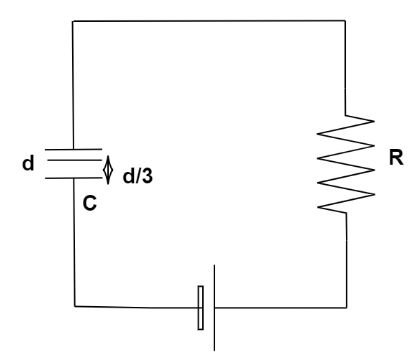
A parallel plate capacitor $C$ with plates of unit area and separation $d$ is filled with a liquid of dielectric constant $K = 2$ . The level of liquid is $\dfrac{d}{3}$​ initially. Suppose the liquid level decreases at a constant speed $V$ , the time constant as a function of time $t$ is:

A. $\dfrac{{6{\varepsilon _0}R}}{{5d + 3Vt}}$
B. $\dfrac{{\left( {15d + 9Vt} \right){\varepsilon _0}R}}{{2{d^2} - 3dVt - 9{V^2}{t^2}}}$
C. $\dfrac{{6{\varepsilon _0}R}}{{5d - 3Vt}}$
D. $\dfrac{{\left( {15d - 9Vt} \right){\varepsilon _0}R}}{{2{d^2} + 3dVt - 9{V^2}{t^2}}}$

Answer 1

We are asked to find the time constant for the given circuit. We can start by noting down the information given in the question. We are given that a part of the capacitor is filled with a liquid and the other part is not. So, we take this as two capacitors connected in series and find the equivalent capacitance. Once we have the total capacitance of the circuit, we can simply multiply with the resistance of the circuit to get the time constant. This will lead us to our required solution.

Formulas used:
The formula for finding the equivalent capacitance of two capacitors connected in series is given by,
${C_s} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}$
The value of capacitance is found using the formula,
$C = \dfrac{{{\varepsilon _0}A}}{d}$
The time constant of the circuit is given by the formula,
$\tau = CR$
Where $R$ is the resistance of the circuit, $C$ is the equivalent capacitance of the circuit and ${C_1}$ and ${C_2}$ are the individual capacitances.

Complete step by step answer:
Let us start by noting down the data given in the question, the capacitance of the capacitor is given as $C$. The level of liquid that fills a part of the capacitor is $\dfrac{d}{3}$ and the dielectric constant of this liquid is, $K = 2$. We can consider the part of the capacitor filled with the liquid as one capacitor and the rest as another. This allows us to find the equivalent capacitance of the circuit. But before we find the equivalent capacitance, we need to find the values of the individual capacitances. The length till which the liquid is filled is, $\dfrac{d}{3}$ , we can subtract this value and find the level of no liquid. At any time $t$ the level of the liquid will be given as,
${d_1} = \dfrac{d}{3} - Vt$

Now to find the value of level of the capacitor not filled with liquid will be,

\Rightarrow {d_2} = \dfrac{{2d}}{3} + Vt$$ Now that we have the levels, we can find the individual capacitances using the formula, $$C = \dfrac{{{\varepsilon _0}A}}{d}$$ The value of capacitance of the liquid free area is found to be, $${C_1} = \dfrac{{{\varepsilon _0}A}}{d} \\\ \Rightarrow {C_1} = \dfrac{{{\varepsilon _0}}}{{\left( {\dfrac{{2d}}{3}} \right) + Vt}}$$ The value of capacitance of the liquid filled area is found to be, $${C_2} = \dfrac{{{\varepsilon _0}A}}{d} \\\ \Rightarrow {C_2} = \dfrac{{2{\varepsilon _0}}}{{\left( {\dfrac{d}{3}} \right) - Vt}}$$ Now we can find the equivalent capacitance of the circuit by using the formula, $${C_s} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}$$ Substituting the values of the individual capacitances we get $${C_s} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} \\\ \Rightarrow {C_s} = \dfrac{{\dfrac{{{\varepsilon _0}}}{{\left( {\dfrac{{2d}}{3}} \right) + Vt}} \times \dfrac{{2{\varepsilon _0}}}{{\left( {\dfrac{d}{3}} \right) - Vt}}}}{{\dfrac{{{\varepsilon _0}}}{{\left( {\dfrac{{2d}}{3}} \right) + Vt}} + \dfrac{{2{\varepsilon _0}}}{{\left( {\dfrac{d}{3}} \right) - Vt}}}} \\\ \Rightarrow {C_s} = \dfrac{{\dfrac{{2{\varepsilon _0}^2}}{{\dfrac{{2{d^2}}}{9} + \dfrac{{dVt}}{3} - {V^2}{t^2}}}}}{{\dfrac{{5{\varepsilon _0}\dfrac{d}{3} + {\varepsilon _0}vt}}{{\dfrac{{2{d^2}}}{9} + \dfrac{{dVt}}{3} - {V^2}{t^2}}}}} \\\ \Rightarrow {C_s} = \dfrac{{6{\varepsilon _0}}}{{5d + 3Vt}}$$ Now that we have the value of capacitance of the circuit, we can find the value of time constant using the formula, $$\tau = CR$$. Substituting we get, $$\tau = CR \\\ \Rightarrow \tau = \dfrac{{6{\varepsilon _0}}}{{5d + 3Vt}} \times R \\\ \therefore \tau = \dfrac{{6{\varepsilon _0}R}}{{5d + 3Vt}}$$ **Therefore, the correct answer is option A.** **Note:** Time constant of a circuit is defined as the time required for a current turned into a circuit under a steady emf or electromotive force to reach $$0.632$$ of its final strength. When we have found the level of liquid at any moment of time, we subtracted the value of the product of the given speed and time because we could get the proper distance or length of the liquid level.