Question

A parallel L-C circuit comprises an $5H$ inductor and $5\mu F$ capacitor calculates the resonant frequency of the circuit.

Answer 1

To solve this question we use the resonant condition for L-C parallel circuit which is given as when inductive and capacitive reactance is equal in magnitude.
${X_L} = {X_C}$
Where ${X_L} \Rightarrow$ inductive reactance of inductor
${X_{C }} \Rightarrow$ Capacitive reactance of capacitor

Complete step by step answer:
First we connect a $5H$ inductor and $5\mu F$ capacitor in parallel to a supply as shown in figure.

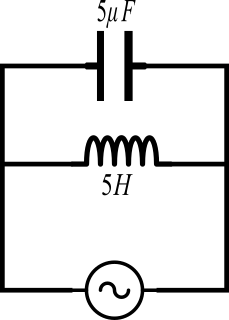
At the resonant condition the inductive and capacitive reactance of inductor and capacitor must be equal
$\Rightarrow {X_L} = {X_C}$
Where ${X_L} = \omega L$
And ${X_C} = \dfrac{1}{{\omega C}}$
According to resonant condition $\Rightarrow {X_L} = {X_C}$
$\Rightarrow \omega L = \dfrac{1}{{\omega C}}$.......................... (1)
In question given $L = 5H$ and $C = 5\mu F$
We know $1\mu F = {10^{ - 6}}F$
So $C = 5 \times {10^{ - 6}}F$
Put these value in (1)
$\Rightarrow \omega \times 5 = \dfrac{1}{{\omega \times 5 \times {{10}^{ - 6}}}}$
Again solving
$\Rightarrow {\omega ^2} = \dfrac{1}{{5 \times 5 \times {{10}^{ - 6}}}}$
$\Rightarrow {\omega ^2} = \dfrac{1}{{25 \times {{10}^{ - 6}}}}$
$\Rightarrow {\omega ^2} = \dfrac{{1 \times {{10}^6}}}{{25}}$
Further solving...
$\Rightarrow \omega = \sqrt {\dfrac{{1 \times {{10}^6}}}{{25}}}$
$\Rightarrow \omega = \dfrac{{1 \times {{10}^3}}}{5}$
$\Rightarrow \omega = \dfrac{{1000}}{5} = 200$
Where $\omega \Rightarrow$ is the angular frequency
We know $\omega = 2\pi f$ where $f \Rightarrow$ resonant frequency
$\Rightarrow \omega = 2\pi f = 200$
$\Rightarrow f = \dfrac{{200}}{{2\pi }}$
Put the value of $\pi = 3.14$
$\Rightarrow f = \dfrac{{200}}{{2 \times 3.14}} = 31.84Hz$
$\therefore f = 31.84Hz$ Is the resonant frequency.

Hence the resonant frequency of this parallel circuit is $31.84Hz$.

Note:
There are two type of resonant circuit one is L-C-R series resonant circuit and other is parallel resonant circuit the resonant frequency formula for both circuit is same but there is some basic difference between them at the resonant condition series resonant circuit has very low resistance and current maximum act as a acceptor circuit. But the parallel resonant circuit at the resonant condition circuit has maximum resistance and minimum current and acts as a rejector circuit.