Question

A parallel beam of monochromatic light of wavelength $500$ $nm$ is incident on a single narrow slit of width $0.001$ $mm$. The light is focussed by a convex lens on a screen placed on the focal plane. The first minimum will be formed for the angle of diffraction equal to
A. $20^\circ$
B. $15^\circ$
C. $30^\circ$
D. $50^\circ$

Answer 1

The light will diffract and the points on the slits will act as secondary sources. The light will hit the surface of the lens and will refract. Consider the pattern formed on the screen due to the interference of the light rays. Apply the condition for the interference to be destructive as a minimum is required.

Complete step by step answer:
The focal plane is a plane associated with the lens. This plane passes through the focus of the lens and the principal axis of the lens is normal to this plane (try to imagine). Consider two light rays, one which comes from the point of slit and the other which comes from the center of the slit. These two considered rays will meet at the focus of the lens and a maximum will be formed on the screen.

Now, consider a point P at the screen where the waves meeting at that point are originating from different points of the slit at an angle $\theta$. Draw a line perpendicular to these parallel rays from the upper edge of the slit. You can see that this perpendicular line also represents the wavefront. After this, the path of every ray will be the same. The only path difference that will occur is the green part as shown in the figure.

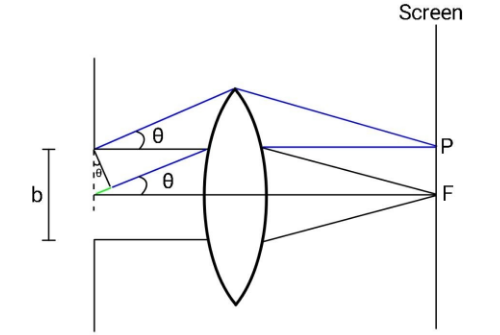
To find this path difference, consider the triangle containing the half-slit width $\dfrac{b}{2}$ and the drawn perpendicular line. From there, using trigonometry, we have the path difference $\Delta x = \dfrac{b}{2}\sin \theta$.

Now, consider the angle $\theta$ for which the path difference is $\dfrac{\lambda }{2}$.Then the phase difference will be $\dfrac{{2\pi }}{\lambda }\dfrac{\lambda }{2} = \pi$.As you can see that the waves will cancel each other. In a similar way, each ray from the upper part of the slit will be cancelled by the lower part of the slit which is at a distance of $\dfrac{b}{2}$. Hence, we can say that by making such pairs, the overall interferences at the point P will be minimum. This is the condition for the first minima.

Hence, we have
$\dfrac{b}{2}\sin \theta = \dfrac{\lambda }{2} \\\ \Rightarrow \sin \theta = \dfrac{\lambda }{b}$
Here, $\lambda$ is the wavelength of the light used. Substituting the given values of $\lambda$ and $b$ from the question in the above derived expression for the angle of diffraction, we get,
$\sin \theta = \dfrac{{500 \times {{10}^{ - 9}}}}{{0.001 \times {{10}^{ - 3}}}} \\\ \Rightarrow \sin \theta = \dfrac{1}{2}$
$\theta = 30^\circ$
Therefore, the first minimum will be formed for the angle of diffraction equal to $30^\circ$.

Hence, option C is correct.

Note: First of all, always remember to convert the units of the provided data appropriately. Remember the method we used to determine the angle of diffraction. Also keep in mind the analysis we made while solving the question, the cancellation of one wave in the upper part by the wave of lower part, the rays which are considered in order to get the path difference. Also remember the trick used to find the path difference, the perpendicular line drawn by us.