Question
Question: A parallel beam of light falls on a convex lens. The path of the rays is shown in the figure. It fol...
A parallel beam of light falls on a convex lens. The path of the rays is shown in the figure. It follows that
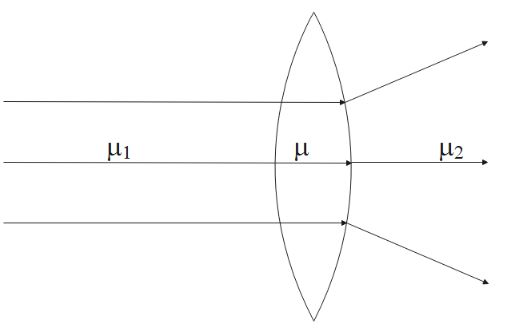
A. μ1>μ>μ2
B. μ2<μ<μ1
C. μ1=μ<μ2
D. μ1=μ>μ2
Solution
This question utilizes the concept of refraction. When a ray of light travels from one medium to another of different refractive indexes, the speed of light changes. This causes the ray of light to bend. But, if the ray travels from one medium to another without any change in refractive index, light does not bend.
Complete step by step answer:
When light passes from a denser to a rarer ( less dense ) substance, (for example passing from water into air), the light is refracted (or bent) away from the normal. Similarly, when it passes from a rarer to a denser substance, it bends towards the normal.
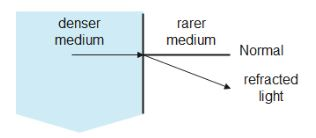
The normal is a line perpendicular (forming a 90 degree angle) to the boundary (contact surface) between the two substances. The bending occurs because light travels more slowly in a denser medium and faster in a rarer medium.
Let The medium with refractive index μ1 be medium1, μ be medium2 and μ2 be medium3
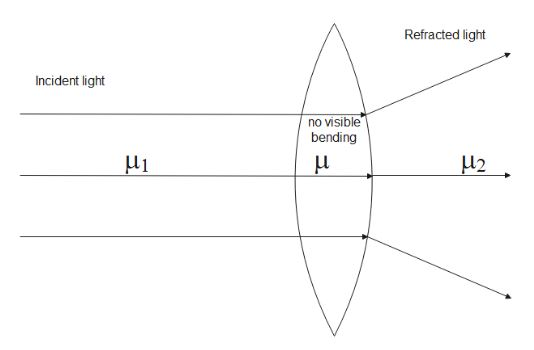
From this figure, we can see that when the incident light passes from medium1 to medium2 , there is no deviation, which means that
μ1=μ ------------(i)
Now, when the ray passes from medium2 to medium3 , it gets refracted. By observing closely, we can see that the ray diverges from the lens.
If the ray was converging, we could have said that μ>μ2
Since they are diverging,
μ<μ2 -----------(ii)
Merging eq (i) and (ii), we get
μ1=μ<μ2
Therefore, the correct option is C.
Note: When a ray travels through the optical centre of any lens, it passes through the lens symmetrically and undeviated. This is because it passes through the normal of the intersecting medium. Thus, in the figure, the ray passing through the between of the lens does not get deviated.
