Question

A parachute is descending vertically and makes angle of elevation of ${{45}^{\circ }}$ and ${{60}^{\circ }}$ at two observing points 100 m apart from each other on the left side of itself. Find the maximum height from which he falls on the ground from the just observation point.

Answer 1

Hint:First of all we will suppose a parachute to be A and the point just below the parachute on the ground will be B. Now, we will take two points C and D from where the angle of elevation are ${{45}^{\circ }}$ and ${{60}^{\circ }}$ respectively and the distance between two points CD is given as $100m$. Then we will use the trigonometric ratio to calculate the required height and distance.

Complete step-by-step answer:
We have been given a parachute makes angles of elevation of ${{45}^{\circ }}$ and ${{60}^{\circ }}$ at two observing points 100 m apart from each other.

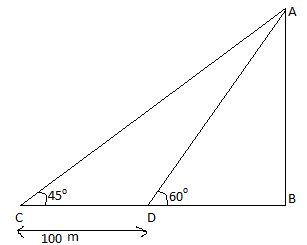
Let us suppose the parachute at point A and the point just below on the ground is B. The two observing points C and D 100 m apart from where angle of elevation are ${{45}^{\circ }}$ and ${{60}^{\circ }}$ respectively.
Let us consider $\Delta ABC$
$\tan C=\dfrac{AB}{BC}$
Since $\angle C={{45}^{\circ }}$ and $BC=BD+CD=\left( BD+100 \right)m$
$\Rightarrow \tan {{45}^{\circ }}=\dfrac{AB}{BD+100}$
We know that $\tan {{45}^{\circ }}=1$.
Substituting in above equation, we get
$\Rightarrow 1=\dfrac{AB}{BD+100}$
On cross multiplication, we get as follows:

& \Rightarrow BD+100=AB \\\ & \Rightarrow BD=AB-100......(1) \\\ \end{aligned}$$ Now in $$\Delta ABD$$, we have, $$\tan D=\dfrac{AB}{BD}$$ Since $$\angle D={{60}^{\circ }}$$ and $$BD=AB-100$$ from equation (1). $$\Rightarrow \tan {{60}^{\circ }}=\dfrac{AB}{AB-100}$$ We know that $$\tan {{60}^{\circ }}=\sqrt{3}$$. $$\Rightarrow \sqrt{3}=\dfrac{AB}{AB-100}$$ On cross multiplication, we get as follows: $$\begin{aligned} & AB\sqrt{3}-100\sqrt{3}=AB \\\ & AB\sqrt{3}-AB-100\sqrt{3}=0 \\\ & AB\left( \sqrt{3}-1 \right)=100\sqrt{3} \\\ & \Rightarrow AB=\dfrac{100\sqrt{3}}{\sqrt{3}-1} \\\ \end{aligned}$$ On rationalizing the denominator, we get as follows: $$AB=\dfrac{100\sqrt{3}\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}-1 \right)\left( \sqrt{3}+1 \right)}$$ Since we know that $$\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$$. $$\begin{aligned} & \Rightarrow AB=\dfrac{100\sqrt{3}\left( \sqrt{3}+1 \right)}{{{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}}} \\\ & \Rightarrow AB=\dfrac{100\sqrt{3}\left( \sqrt{3}+1 \right)}{3-1} \\\ & \Rightarrow AB=\dfrac{100\sqrt{3}\left( \sqrt{3}+1 \right)}{2} \\\ & \Rightarrow AB=50\sqrt{3}\left( \sqrt{3}+1 \right) \\\ \end{aligned}$$ We know that $$\sqrt{3}=1.732$$. $$\begin{aligned} & \Rightarrow AB=50\times 1.732\left( 1.732+1 \right) \\\ & \Rightarrow AB=236.6m \\\ \end{aligned}$$ $\therefore$ we get maximum height from which he falls is $AB=236.6m$ Now substituting the value of AB in equation (1) we get the distance of the point where he falls i.e $$BD=236.6-100=136.6m$$ Therefore, the maximum height is 236.6 m and the distance of the point where he falls on the ground from just the observation point is 136.6 m. Note: In this type of question, we must have to draw a diagram according to the condition given in the question and then move further for calculation. Also, be careful while drawing the diagram and mark the angle correctly according to the question as they are given that angles are made with respect to ground.Also, don’t get confused about the value of $$\tan {{60}^{\circ }}$$. Sometimes we use $$\tan {{60}^{\circ }}=\dfrac{1}{\sqrt{3}}$$ and $$\tan {{30}^{\circ }}=\sqrt{3}$$ which is wrong. So take care of it while calculating.Students should remember the important trigonometric ratios and standard angles to solve these types of questions.