Question

A parabola touches two given straight lines at given points; prove that the locus of the middle point of the portion of the tangent which is intercepted between the given straight lines is a straight line.

Answer 1

The figure representing the given data is

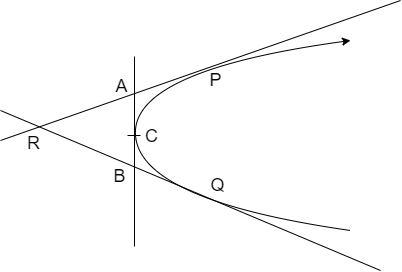
We assume that the equation of parabola as ${{y}^{2}}=4ax$ then we use the standard result of point of intersection of two tangents that is if the tangent drawn from $P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ intersect at $'R'$ then the co – ordinates of point $'R'$ is given as
$\Rightarrow R=\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$
By using the above result we find the locus of point $\left( h,k \right)$ which is the midpoint of $A, B$

Complete step-by-step solution:
Let us assume that the equation of parabola as
$\Rightarrow {{y}^{2}}=4ax$
We are given that tangents are drawn at given points
Let us assume that the given points as
$\Rightarrow P=\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$
$\Rightarrow Q=\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$
Let us assume that the tangent intercepted between the known tangents touches the parabola at
$C\left( at,2at \right)$
We know that the standard result of point of intersection of tangents of parabola that is if the tangent drawn from $P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ intersect at $'R'$ then the co – ordinates of point $'R'$ is given as
$\Rightarrow R=\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$
By using the above result the point of intersection of tangents drawn from $'P'$ and $'C'$ is given as
$\Rightarrow A=\left( at{{t}_{1}},a\left( t+{{t}_{1}} \right) \right)$
Similarly, we can have the point of intersection of tangents drawn from $'Q'$ and $'C'$ is given as
$\Rightarrow B=\left( at{{t}_{2}},a\left( t+{{t}_{2}} \right) \right)$
Now, let us assume that the mid – point of $A,B$ as $D\left( h,k \right)$
We know that the co – ordinates of mid – point $'D'$ between $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as
$\Rightarrow D=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
By using the above formula to points $A,B$ we get
$\Rightarrow \left( h,k \right)=\left( \dfrac{at\left( {{t}_{1}}+{{t}_{2}} \right)}{2},\dfrac{2at+a\left( {{t}_{1}}+{{t}_{2}} \right)}{2} \right)$
Now, by equating the X co – ordinates we get

& \Rightarrow h=\dfrac{at\left( {{t}_{1}}+{{t}_{2}} \right)}{2} \\\ & \Rightarrow at=\dfrac{2h}{\left( {{t}_{1}}+{{t}_{2}} \right)}.....equation(i) \\\ \end{aligned}$$ Similarly, by equating the Y co – ordinates we get $$\begin{aligned} & \Rightarrow k=\dfrac{2at+a\left( {{t}_{1}}+{{t}_{2}} \right)}{2} \\\ & \Rightarrow 2at=2k-a\left( {{t}_{1}}+{{t}_{2}} \right) \\\ & \Rightarrow at=k-\dfrac{a\left( {{t}_{1}}+{{t}_{2}} \right)}{2}.........equation(ii) \\\ \end{aligned}$$ Now, let us subtract equation (ii) from equation (i) then we get $$\begin{aligned} & \Rightarrow \dfrac{2h}{\left( {{t}_{1}}+{{t}_{2}} \right)}-\left[ k-\dfrac{a\left( {{t}_{1}}+{{t}_{2}} \right)}{2} \right]=0 \\\ & \Rightarrow \dfrac{2h}{\left( {{t}_{1}}+{{t}_{2}} \right)}-k+\dfrac{a\left( {{t}_{1}}+{{t}_{2}} \right)}{2}=0 \\\ \end{aligned}$$ By doing the LCM and cross multiplying the above equation we get $$\Rightarrow 4h-2k\left( {{t}_{1}}+{{t}_{2}} \right)+a{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}=0$$ Now, we have the locus of mid – point of $$A,B$$ by replacing the values of $$\left( h,k \right)$$ by $$\left( x,y \right)$$ So, the locus of mid – point $$'D'$$ is given as $$\Rightarrow 4x-2y\left( {{t}_{1}}+{{t}_{2}} \right)+a{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}=0$$ Here, we can see that the above equation is a straight line. Hence the required result has been proved that the locus of the middle point of the portion of the tangent which is intercepted between the given straight lines is a straight line. **Note:** Students may make mistakes at the point $$'C'$$ that is in the figure the point $$'C'$$ is assumed to be the midpoint of $$A, B$$ which will be wrong. We got the rough figure as that type, but it is not necessary that the point $$'C'$$ is the midpoint of $$A, B$$ Also we have the point of intersection of two tangents that is if the tangent drawn from $$P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$$ and $$Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$$ intersect at $$'R'$$ then the co – ordinates of point $$'R'$$ is given as $$\Rightarrow R=\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$$ The above-mentioned formula is applicable only for the parabola of equation $${{y}^{2}}=4ax$$ but not for all parabolas. This point is important because students may use the above formula for all parabolas.