Question

A parabola touches the sides of a triangle ABC in the points D, E, and F respectively; if DE and DF cut the diameter through the point A in b and c respectively, prove that Bb and Cc are parallel.

Answer 1

Let us assume ${{y}^{2}}=4ax$ is a parabola touching the three sides BC, CA, and AB of a triangle ABC at D, E and F respectively. We know that the equation of tangent at a point P $\left( {{x}_{1}},{{y}_{1}} \right)$ to parabola ${{y}^{2}}=4ax$ is ${{S}_{1}}=0$. We know that the diameter of a parabola is parallel to the axis of the parabola. By using these concepts and by illustrating the correct diagram, students can solve the question.

Complete step-by-step solution
Let us assume ${{y}^{2}}=4ax$ is a parabola touching the three sides BC, CA, and AB of a triangle ABC at D, E, and F respectively.

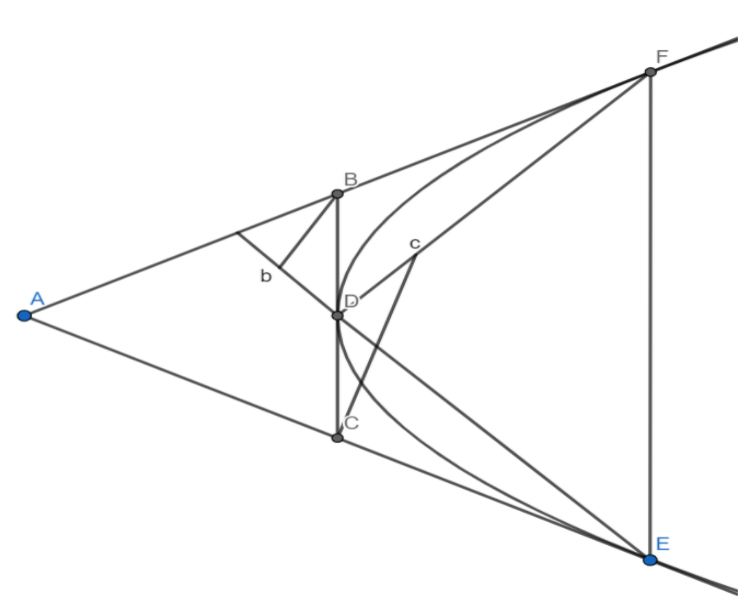
The general form of a point on a parabola ${{y}^{2}}=4ax$ is $\left( a{{t}^{2}},2at \right)$. As the points D, E and F are on parabola, they can be written as $D\left( at_{1}^{2},2a{{t}_{1}} \right)$, $E\left( at_{2}^{2},2a{{t}_{2}} \right)$and $F\left( at_{3}^{2},2a{{t}_{3}} \right)$.
The tangents of the parabola at points D, E, and F represent the sides of triangle BC, CA, and AB respectively.
We know that the equation of tangent at a point $P\left( {{x}_{1}},{{y}_{1}} \right)$ to parabola ${{y}^{2}}=4ax$ is ${{S}_{1}}=0$.$\Rightarrow {{S}_{1}}=0\Leftrightarrow y{{y}_{1}}=2ax+2a{{x}_{1}}\Leftrightarrow y\left( 2at \right)=2ax+2{{a}^{2}}{{t}^{2}}$.
$\Rightarrow ty=x+a{{t}^{2}}$.
$\Rightarrow x-ty+a{{t}^{2}}=0$.
Now we should find the tangents at D, E and F. Let us assume the tangents at D, E, and F are represented by equations (1), (2), and (3) respectively.
$\Rightarrow x-{{t}_{1}}y+a{{t}_{1}}^{2}=0\to \left( 1 \right)$.
$\Rightarrow x-{{t}_{2}}y+a{{t}_{2}}^{2}=0\to \left( 2 \right)$.
$\Rightarrow x-{{t}_{3}}y+a{{t}_{3}}^{2}=0\to \left( 3 \right)$.
By solving equation (2) and equation (3), vertex A of triangle ABC is obtained.

& x-{{t}_{2}}y+a{{t}_{2}}^{2}=0 \\\ & x-{{t}_{3}}y+a{{t}_{3}}^{2}=0 \\\ & ........................... \\\ & \left( {{t}_{3}}-{{t}_{2}} \right)y+a\left( t_{2}^{2}-t_{3}^{2} \right)=0 \\\ \end{aligned}$$ $$\Rightarrow \left( {{t}_{3}}-{{t}_{2}} \right)y=a\left( t_{3}^{2}-t_{2}^{2} \right)$$. $$\Rightarrow y=a\left( {{t}_{3}}+{{t}_{2}} \right)\to \left( 4 \right)$$. Now let us substitute equation (4) in equation (2) $$\Rightarrow x-{{t}_{2}}\left( a\left( {{t}_{3}}+{{t}_{2}} \right) \right)+at_{2}^{2}=0$$. $$\Rightarrow x=a{{t}_{2}}{{t}_{3}}\to \left( 5 \right)$$. From equation (4) and equation (5), the vertex A is $$A\left( a{{t}_{2}}{{t}_{3}},a\left( {{t}_{3}}+{{t}_{2}} \right) \right)$$. In the similar manner, vertex B and vertex C is $$\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$$and $$\left( a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right)$$ respectively. We know that the diameter of a parabola is parallel to the axis of the parabola. Hence, the diameter though A is parallel to axis of parabola and the equation of diameter through A is $$y=a\left( {{t}_{2}}+{{t}_{3}} \right)\to \left( 6 \right)$$. Given that the point of intersection of DE and equation of diameter through A is b and point of intersection of DF and equation of diameter through A is c. Equation of DE is $$y-2a{{t}_{1}}=\left( \dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}} \right)\left( x-at_{1}^{2} \right)$$. $$\Rightarrow y-2a{{t}_{1}}=\left( \dfrac{2}{{{t}_{1}}+{{t}_{2}}} \right)\left( x-at_{1}^{2} \right)$$. $$\Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)\left( y-2a{{t}_{1}} \right)=2\left( x-at_{1}^{2} \right)$$. $$\Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)y-2a{{t}_{1}}\left( {{t}_{1}}+{{t}_{2}} \right)=2x-2at_{1}^{2}$$. $$\Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)y-2a{{t}_{1}}{{t}_{2}}=2x$$. $$\Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)y=2a{{t}_{1}}{{t}_{2}}+2x\to \left( 7 \right)$$. Now, let us substitute equation (6) in equation (7) The coordinates of b are $$b\left( \dfrac{a\left( t_{2}^{2}+{{t}_{1}}{{t}_{3}}+{{t}_{2}}{{t}_{3}}-{{t}_{1}}{{t}_{2}} \right)}{2},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)$$. In the similar manner, the equation of DF is $$\left( {{t}_{1}}+{{t}_{3}} \right)y=2a{{t}_{1}}{{t}_{3}}+2x\to \left( 8 \right)$$ Now, let us substitute equation (6) in equation (8) The coordinates of c are $$c\left( \dfrac{a\left( t_{3}^{2}+{{t}_{1}}{{t}_{2}}+{{t}_{2}}{{t}_{3}}-{{t}_{1}}{{t}_{3}} \right)}{2},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)$$. The slope of Bb is $${{m}_{1}}$$ and the slope of Cc is $${{m}_{2}}$$. $$\Rightarrow {{m}_{1}}=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( t_{2}^{2}+{{t}_{2}}{{t}_{3}}-{{t}_{1}}{{t}_{3}}-{{t}_{1}}{{t}_{2}} \right)}=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}-{{t}_{3}} \right)}=\dfrac{2}{\left( {{t}_{2}}-{{t}_{3}} \right)}$$. In the same manner, the slope of Cc is $${{m}_{2}}=\dfrac{2}{\left( {{t}_{2}}-{{t}_{3}} \right)}$$. If two slopes are equal, then the lines are said to be parallel. As the slopes of Bb and Cc are equal, Bb is parallel to Cc. Hence, the given statement is proved. **Note:** If students are unable to illustrate the diagram, then we cannot get an idea to have a good approach to this problem. So, the diagram should be illustrated in the correct manner. Students may have a misconception that the diameter of the parabola is perpendicular to the axis of the parabola. But we know that the diameter of the parabola is parallel to the axis of the parabola. So, students should have a clear view of this concept.