Question
Question: A parabola is drawn to pass through \[A\] and \[B\], the ends of a diameter of a given circle of rad...
A parabola is drawn to pass through A and B, the ends of a diameter of a given circle of radius a and to have as directrix a tangent to a concentric circle of radius b; the axes being AB and a perpendicular diameter, prove that the locus of the focus of the parabola is b2x2+b2−a2y2=1.
Solution
Hint: Any point on the parabola is equidistant from the focus and directrix.
Let the equation of the circle be x2+y2=a2.....(i)
In the question, it is given that A and B are the ends of the diameter of the circle.
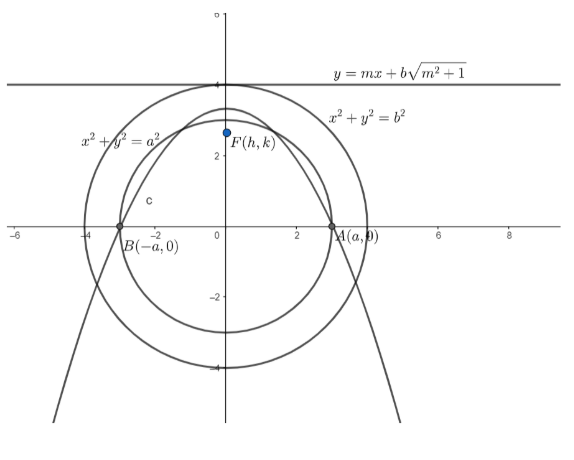
So, let A=(a,0) and B=(−a,0)
In the question, it is given that the radius of the concentric circle is b.
So, let the equation of concentric circle be x2+y2=b2....(ii)
Now, the directrix of the parabola is tangent to the concentric circle.
First, we find the equation of tangent to the concentric circle.
We know, the equation of tangent to a circle x2+y2=r2 in slope form is given as y=mx±r1+m2.
So, equation of tangent to (ii)is
y=mx+bm2+1
Or mx−y+bm2+1=0....(iii)
Equation (iii) is also the directrix to the parabola.
Now, we want to find the locus of the focus of the parabola.
So, let the focus of the parabola be F(h,k).
Now, by the definition of a parabola, any point on the parabola is equidistant from the focus and the directrix.
Now, from the question, we know that the ends of diameter of (i)i.e. A and B lie on the parabola.
We know that the distance between two points (x1,y1) and (x2,y2) is given as d=(x1−x2)2+(y1−y2)2 and the distance of a point (x1,y1) from the line lx+my+n=0 is given
as d=l2+m2lx1+my1+n.
So, for A(a,0), we have
(h−a)2+k2=m2+1m(a)−1(0)+bm2+1
⇒(h−a)2+k2=m2+1am+bm2+1....(iv)
For B(−a,0), we have
(h+a)2+k2=m2+1m(−a)−1(0)+bm2+1
⇒(h+a)2+k2=m2+1−am+bm2+1....(v)
Adding (iv)and (v), we have
(h−a)2+k2+(h+a)2+k2=m2+12bm2+1
⇒(h−a)2+k2+(h+a)2+k2=2b
(h+a)2+k2=2b−(h−a)2+k2
Now, on squaring both sides we get,
h2+2ah+a2+k2=4b2+h2−2ah+a2+k2−4b(h−a)2+k2
