Question

A parabola has its vertex and focus in the first quadrant and axis along the line $y = x$. If the distances of the vertex and focus from the origin are respectively $\sqrt 2$and $2\sqrt 2$ , then an equation of the parabola is
A. ${\left( {x + y} \right)^2} = x - y + 2$
B. ${\left( {x - y} \right)^2} = x + y - 2$
C. ${\left( {x - y} \right)^2} = 8\left( {x + y - 2} \right)$
D. ${\left( {x + y} \right)^2} = 8\left( {x - y + 2} \right)$

Answer 1

At first we will find the coordinates of the vertex and the focus of the parabola as we have given that they lie on the line $y = x$ and their distance from the origin. From these points and the equation of axis, we will find the equation of the directrix of the parabola as the directrix and the focus of the parabola are equidistant from the vertex. As we know that the directrix and the focus of the parabola are the equidistant any random point of the parabola so from this we will find the equation of the required parabola.

Complete step by step answer:

Given data: The axis of a parabola is along the line $y = x$.
The distances of the vertex and focus from the origin are respectively $\sqrt 2$ and $2\sqrt 2$

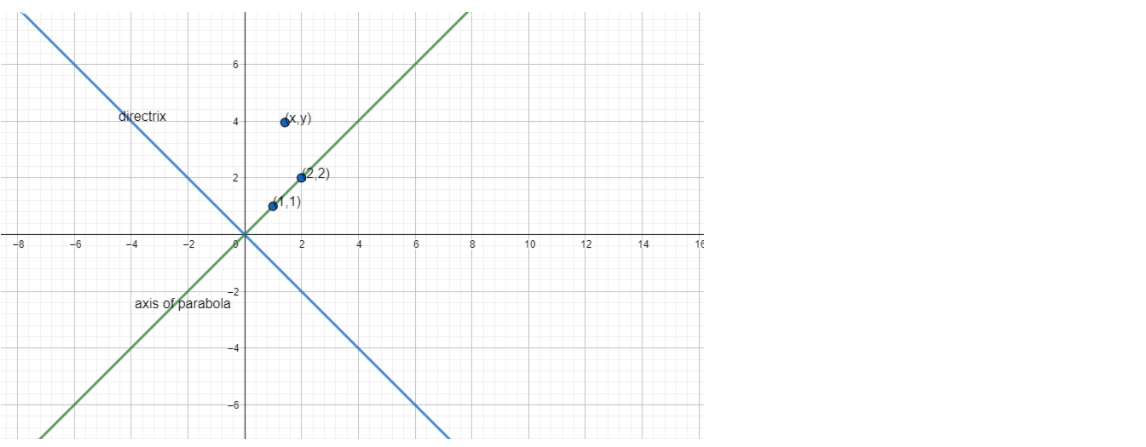
Since the axis of the parabola is $y = x$
Therefore ordinate and abscissa of any point will be equal
Now, let the vertex of the parabola be $(a,a)$ and the focus be $(b,b)$
Now we know that the distance formula states that distance between any two points $\left( {l,m} \right)$ and $\left( {p,q} \right)$is given by $\sqrt {{{\left( {q - m} \right)}^2} + {{\left( {p - l} \right)}^2}}$ .
Therefore the distance between the vertex of the parabola and origin will be $\sqrt {{{\left( {a - 0} \right)}^2} + {{\left( {a - 0} \right)}^2}}$
And it is given $\sqrt 2$
i.e. $\sqrt {{{\left( {a - 0} \right)}^2} + {{\left( {a - 0} \right)}^2}} = \sqrt 2$
On squaring both sides we get,
$\Rightarrow 2{a^2} = 2$
On Dividing by 2 we get,
$\therefore a = 1$ , here we have taken the positive part as we have given that the points lie on the first quadrant.
Similarly, the distance between the focus of the parabola and origin will be $\sqrt {{{\left( {b - 0} \right)}^2} + {{\left( {b - 0} \right)}^2}}$
And it is given $2\sqrt 2$
i.e. $\sqrt {{{\left( {b - 0} \right)}^2} + {{\left( {b - 0} \right)}^2}} = 2\sqrt 2$
On squaring both sides we get,
$\Rightarrow 2{b^2} = 8$
On Dividing by 2 we get,
$\therefore b = 2$ , here we have takn the positive part as we have given that the points lie on the first quadrant.
Therefore coordinate of the vertex will be $(1,1)$ and focus will be $(2,2)$
And the midpoint formula states that if $\left( {x,y} \right)$ is the midpoint of $\left( {l,m} \right)$ and $\left( {p,q} \right)$
Then, $\left( {x,y} \right) = \left( {\dfrac{{l + p}}{2},\dfrac{{m + q}}{2}} \right)$
We know that on a parabola vertex is the midpoint of focus and the directrix at the axis
Now let coordinate of directrix at vertex be $\left( {c,c} \right)$
Therefore, $\left( {1,1} \right) = \left( {\dfrac{{c + 2}}{2},\dfrac{{c + 2}}{2}} \right)$
On comparing we get, $1 = \dfrac{{c + 2}}{2}$
On cross multiplication and simplification we get, $c = 0$
Therefore point at which the axis of parabola and the directrix meet is $\left( {0,0} \right)$
The general equation of a line is given by $y = mx + k$ , where m is the slope and k is a constant
on comparing the axis of parabola with general equation of line
slope of the axis of the parabola $= 1$
we know that product of slpoes of two perpendicular lines is equal to -1 and the the axis of the parabola and the directrix are perpendicular to each other
therefore slope of directrix is -1.
And the equation of directrix will be $y + x = 0$ as it passes through the origin
Now we know that any point on the parabola is equidistant from the focus and the directrix
Let a point from the locus of points of parabola be given by $(x,y)$
$\Rightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 2} \right)}^2}} = \dfrac{{\left| {x + y} \right|}}{{\sqrt 2 }}$
On Squaring both sides we get,
$\Rightarrow {\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = \dfrac{{{{\left( {x + y} \right)}^2}}}{2}$
Opening the square brackets we get,
$\Rightarrow {x^2} + 4 - 4x + {y^2} + 4 - 4y = \dfrac{{{x^2} + {y^2} + 2xy}}{2}$
Multiplying the equation by 2 and simplifying we get,
$\Rightarrow {x^2} + 16 - 8x + {y^2} - 8y - 2xy = 0$
On rearranging we get,
$\Rightarrow {x^2} + {y^2} - 2xy = 8x + 8y - 16$
Using ${x^2} + {y^2} - 2xy = {\left( {x - y} \right)^2}$ , we get,
$\Rightarrow {\left( {x - y} \right)^2} = 8\left( {x + y - 2} \right)$

Hence, Option (C) is correct.

Note: While finding the coordinates of the vertex and the focus of the parabola we can use an alternative method i.e.
We know the equation of axis is $y = x$ where slope is 1
Or we can say that, $\tan \theta = 1$
$\Rightarrow \tan \theta = \tan \dfrac{\pi }{4}$
$\therefore \theta =\dfrac{\pi }{4}$
We know that coordinate of any point is $\left( {r\cos \theta ,r\sin \theta } \right)$ where r is the distance from origin and theta is the angle from positive x-axis
Coordinate of vertex will be $\left( {\sqrt 2 \cos \dfrac{\pi }{4},\sqrt 2 \sin \dfrac{\pi }{4}} \right)$
$\Rightarrow \left( {\sqrt 2 \dfrac{1}{{\sqrt 2 }},\sqrt 2 \dfrac{1}{{\sqrt 2 }}} \right)$
$\Rightarrow \left( {1,1} \right)$
And Coordinate of focus will be$\left( {2\sqrt 2 \cos \dfrac{\pi }{4},2\sqrt 2 \sin \dfrac{\pi }{4}} \right)$
$\Rightarrow \left( {2\sqrt 2 \dfrac{1}{{\sqrt 2 }},2\sqrt 2 \dfrac{1}{{\sqrt 2 }}} \right)$
$\Rightarrow \left( {2,2} \right)$