Question

Let ABCD be a quadrilateral in which AB || CD, AB ⊥ AD and AB = 3CD. If the area of the quadrilateral is 4, then the radius of the circle touching all the four sides of the quadrilateral is

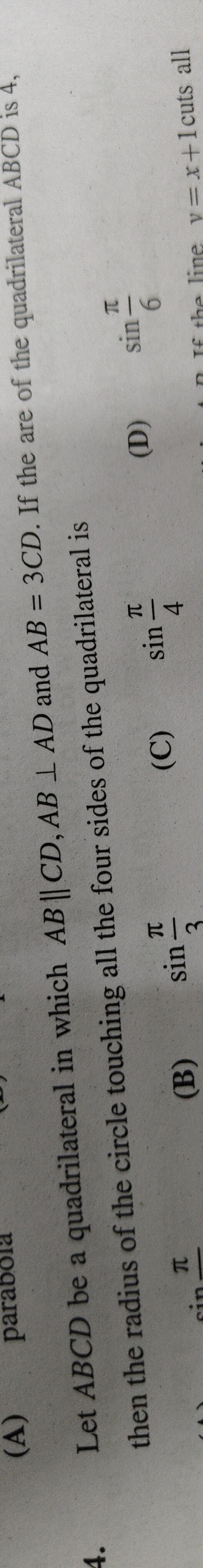
• A. sin(pi/3)
• B. sin(pi/4)
• C. sin(pi/6)
• D. The radius is $\frac{\sqrt{3}}{2}$

Answer 1

Answer: (D)

The radius is $\frac{\sqrt{3}}{2}$

Answer 2

Let CD = x, then AB = 3x. Since AB || CD and AB ⊥ AD, AD is the height of the trapezoid and AD = 2r, where r is the radius of the inscribed circle. The area of the trapezoid is given by: Area = $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$ Given Area = 4, so: $4 = \frac{1}{2} \times (AB + CD) \times AD$ $4 = \frac{1}{2} \times (3x + x) \times (2r)$ $4 = \frac{1}{2} \times (4x) \times (2r)$ $4 = 4xr$ $xr = 1$ (Equation 1)

For a tangential quadrilateral, the sum of opposite sides are equal: AB + CD = BC + AD $3x + x = BC + 2r$ $4x = BC + 2r$ $BC = 4x - 2r$ (Equation 2)

Construct a perpendicular from C to AB, meeting AB at E. Then ADCE forms a rectangle, so AE = CD = x and CE = AD = 2r. The length EB = AB - AE = 3x - x = 2x. In the right-angled triangle CEB, by the Pythagorean theorem: $BC^2 = CE^2 + EB^2$ $BC^2 = (2r)^2 + (2x)^2$ $BC^2 = 4r^2 + 4x^2$ (Equation 3)

Substitute BC from Equation 2 into Equation 3: $(4x - 2r)^2 = 4r^2 + 4x^2$ $16x^2 - 16xr + 4r^2 = 4r^2 + 4x^2$ $16x^2 - 16xr = 4x^2$ $12x^2 - 16xr = 0$ Since x (length of CD) is non-zero, we can divide by 4x: $3x - 4r = 0$ $3x = 4r$ $x = \frac{4}{3}r$ (Equation 4)

Substitute the value of x from Equation 4 into Equation 1: $(\frac{4}{3}r) \times r = 1$ $\frac{4}{3}r^2 = 1$ $r^2 = \frac{3}{4}$ $r = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}$

The calculated radius $r = \frac{\sqrt{3}}{2}$ matches option (B) which is $sin\frac{\pi}{3}$.