Solveeit Logo
Login

Question

Question: A pair of stationary and infinitely long bent wire is placed in the x-y plane as shown in figure. Ea...

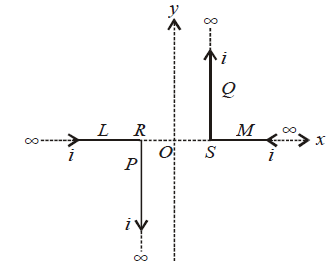
A pair of stationary and infinitely long bent wire is placed in the x-y plane as shown in figure. Each wire carries current of 10A. segments L and M are along the x-axis. Segments P and Q are parallel to the y-axis such that OS=OR=0.02m. find the magnitude and direction of the magnetic induction at origin O in the form of x×10−4x\times { 10 }^{ -4 }. What is x?

Explanation

Solution

Hint: An electric field produces a magnetic field in a series of circles around the wire segment. The Biot – Savart law is used to derive the magnetic strength from a current segment of wire.

Formula used: BR=μ04πIRO+μ04πISO{ B }_{ R }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { I }{ RO } +\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { I }{ SO }

Complete step-by-step solution -
According to electromagnetism, a change in electric field produces a magnetic field at the point around a wire. The given pair of infinitely long wire has 10 segments along x and y axes. O is along the path or length of L and M and so the magnetic field at O because of those segments will be zero. But from the diagram, we can see that O is also near one of the ends of the wire.
So, the resultant field at O can be given as,
BR = BP + BQ
The above-mentioned fields will be within the plane. Let us now apply the Biot-savart law of magnetic field.
Biot-savart law determines the magnetic field generated by current. It relates the magnetic field to the magnitude, direction and length of the current. It is given as,
BR=μ04πIRO+μ04πISO{ B }_{ R }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { I }{ RO } +\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { I }{ SO }
We know RO=SO=0.02m
BR=2×μ04π100.02{ B }_{ R }=2\times \dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { 10 }{ 0.02 }
Where, μ0μ_0 = 4π×10−74\pi \times 10^{-7} and π = 3.14
BR=2×10−7100.02{ B }_{ R }=2\times { 10 }^{ -7 }\dfrac { 10 }{ 0.02 }
On solving. We get,
BR = 1×10−4Wbm−21 \times 10^{-4} {Wbm^{-2}}
Therefore, the value of x = 1 and direction of field is vertically upwards.

Note: The SI unit of magnetic field is tesla and represented as T. Whereas, H also denotes magnetic field and can be represented in amperes per metre (A/m). In the CGS system, it can be measured in unit gauss (G).