Question

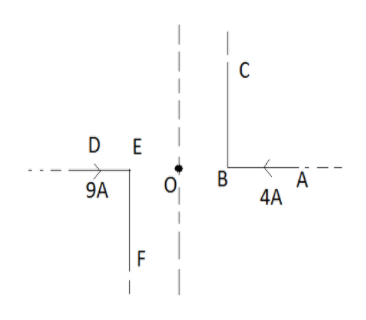
A pair of stationary and infinitely long bent wires are placed in the x-y plane as shown in figure. The two wires carry currents of 4A and 9A respectively. If the segments D and A are along x- axis and the segment and C and F are parallel to y- axis such that OB=2cm and OE=3cm, then the magnitude of magnetic induction at the origin ‘O’ is: (${{\mu }_{0}}=4\pi \times {{10}^{-7}}H{{m}^{-1}}$)

A. $4\times {{10}^{-5}}T$
B. $5\times {{10}^{-5}}T$
C. $6\times {{10}^{-5}}T$
D. $2\times {{10}^{-5}}T$

Answer 1

Hint : Magnetic field due to wire DE and AB at origin O is zero. Because these wires lie on the x axis and subtends angle zero degree at origin. The magnetic field at origin is only due to the infinitely long wire EF and BC. We will find magnetic fields due to infinitely long wire EF and BC individually and final add them as a resultant.
Formula Used:
Biot – Savart Law:
$dB=\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{Idl\sin \theta }{{{r}^{2}}}$
Magnetic field due to infinitely long wire at point O.
$B=\dfrac{{{\mu }_{0}}I}{4\pi a}(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})$

Complete step by step answer:
In our question there are two wires carrying current 9A and 4A respectively. Segment D and A are along the x axis and segment C and F are parallel to the y axis.
It is also given that the distance of two wires from origin i.e. OB=2cm and OE=3cm
Magnetic field at Origin due the wire DE and BA which are along the x axis is zero according to Biot-Savart Law.
Biot-Savart Law According to Biot-Savart Law, the magnetic field due the small current element in the wire at distance r from it is given by:
$dB=\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{Idl\sin \theta }{{{r}^{2}}}$
Where:
$dB=$magnetic field due to small current element
$Idl=$ electric current in the wire
$r=$ distance from the wire where magnetic field is to be determined
$\theta =$angle between current element and r.
In our question the wire along the axis makes angle zero degree with origin therefore $\sin {{0}^{0}}=0$, Hence magnetic field is zero.
Now, magnetic field due to infinitely long wire at distance $a$ from it is given by:
$B=\dfrac{{{\mu }_{0}}I}{4\pi a}(\sin {{\theta }_{1}}+\sin {{\theta }_{2}})$
Where:
${{\theta }_{1}}=$ It is the angle made by external point at starting end of the wire and it is equals to ${{0}^{0}}$
${{\theta }_{2}}=$ it is the angle made by external point at end of the wire ${{90}^{0}}$
Therefore we get the general formula for magnetic field $=\dfrac{{{\mu }_{0}}I}{4\pi a}(\sin {{0}^{0}}+\sin {{90}^{0}})=\dfrac{{{\mu }_{0}}I}{4\pi a}(0+1)=\dfrac{{{\mu }_{0}}I}{4\pi a}$
Magnetic field by infinitely long wire EF:
$=\dfrac{{{\mu }_{0}}I}{4\pi a}$

& =\dfrac{4\pi \times {{10}^{-7}}\times 9}{4\pi \times 3\times {{10}^{-2}}} \\\ & =3\times {{10}^{-5}}T \\\ \end{aligned}$$ Magnetic field by infinitely long wire EF: $$=\dfrac{{{\mu }_{0}}I}{4\pi a}$$ $$\begin{aligned} & =\dfrac{4\pi \times {{10}^{-7}}\times 4}{4\pi \times 2\times {{10}^{-2}}} \\\ & =2\times {{10}^{-5}}T \\\ \end{aligned}$$ By applying the right hand thumb rule direction of the magnetic field by each wire is out of the plane. Therefore the resultant magnetic field is addition of magnetic field by each wire. $$\begin{aligned} & B=3\times {{10}^{-5}}T+2\times {{10}^{-5}}T \\\ & B=5\times {{10}^{-5}}T \\\ \end{aligned}$$ Hence, the magnetic field at origin O is $$5\times {{10}^{-5}}T$$. Therefore the correct answer is option B. Note: Remember to change CGS units to SI units like change cm to m to obtain the correct answer. And remember to pay attention to the direction of the magnetic field by applying the right hand thumb rule. If the direction of magnetic field by both the wires is out or in the paper then add the magnetic field and if the direction is opposite then subtract the individual magnetic field.