Question

(A) Obtain a relation for equivalent capacitance of the series combination of capacitors. Draw circuit diagram.
(B) 10 Capacitors each of capacity $10\mu F$ are joined first in series and then in parallel. Write the value of product equivalent capacitances.
(C) What will be the value of capacitance of a $4\mu F$ capacitor if a dielectric of dielectric constant 2 is inserted fully between the plates of parallel plate capacitor.

Answer 1

Capacitors is defined as a device which has the ability to hold charge. They are required in devices which require a high amount of current for a short period of time. There are two types of combination of capacitors one is in series combination and another one is parallel combination.

Complete step by step solution:
Step 1: The relation for equivalent capacitance of the series combination of capacitors.
When one capacitor’s terminal is connected to another capacitor’s terminal it is called a combination of series of capacitors. Here, the charge on each capacitor remains the same as from the battery flow of charge is the same for each capacitor. There are three capacitors which are in series with each other.

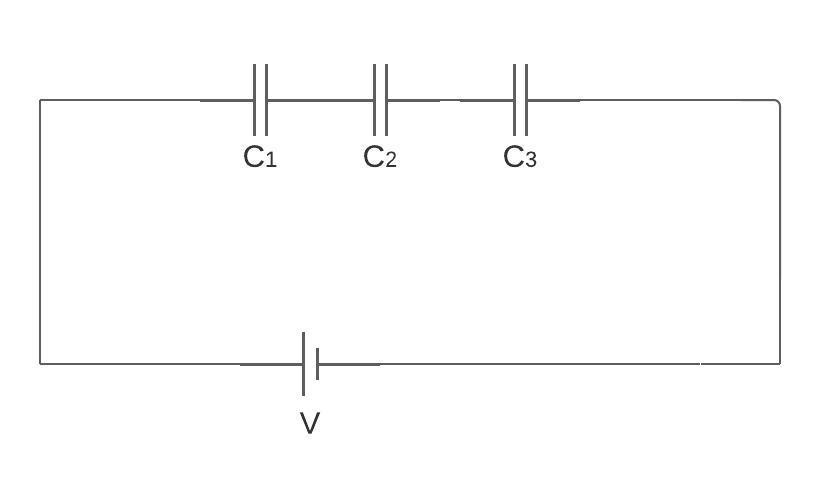
For the first capacitor the charge on it will be: ${Q_1} = {C_1}{V_1}$.
For the second capacitor the charge will be: ${Q_2} = {C_2}{V_2}$.
For the third capacitor the charge will be: ${Q_3} = {C_3}{V_3}$.
As we know that the in series the charge on each capacitor is same:
${Q_1} = {Q_2} = {Q_3}$ and the equivalent capacitance would be $Q = {C_{eq}}V$.
Also,
The equivalent potential would be: $V = {V_1} + {V_2} + {V_3}$.
Now, we know that:
$Q = {C_{eq}}V$.
In terms of voltage we can write above relation as:
$\dfrac{Q}{{{C_{eq}}}} = \dfrac{Q}{{{C_1}}} + \dfrac{Q}{{{C_2}}} + \dfrac{Q}{{{C_3}}}$;
Cancel out the common variable:
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}};$….(Capacitance in series)
Here in the series capacitances the current in each of the capacitance remains the same but the voltage is not. This is the property for the capacitances in series, for capacitance in parallel the voltage in each of the capacitance will remain the same but the current changes for each capacitance.

Step 2: 10 Capacitors each of capacity $10\mu F$ are joined first in series and then in parallel. The value of product equivalent capacitances:
Equivalent capacitance in series:
$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}} + \dfrac{1}{{{C_5}}} + \dfrac{1}{{{C_6}}} + \dfrac{1}{{{C_7}}} + \dfrac{1}{{{C_8}}} + \dfrac{1}{{{C_9}}} + \dfrac{1}{{{C_{10}}}};$
Here all the capacitors are of $10\mu F$so, the equivalent capacitance would be:
$\Rightarrow \dfrac{1}{{{C_s}}} = \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}};$
$\Rightarrow \dfrac{1}{{{C_s}}} = \dfrac{{10}}{{10}}$
Equivalent capacitance in series would be:
${C_s} = 1\mu F$;
Similarly, for capacitors in parallel combination would be:
${C_p} = {C_1} + {C_2} + {C_3} + {C_4} + {C_5} + {C_6} + {C_7} + {C_8} + {C_9} + {C_{10}}$
Here all the capacitors are of $10\mu F$ so, the equivalent capacitance would be:
$\Rightarrow {C_p} = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10$;
$\Rightarrow {C_p} = 100\mu F$;
The product of equivalent capacitance is:
${C_s}{C_p} = {10^{ - 6}} \times 100 \times {10^{ - 6}}$;
$\Rightarrow {C_s}{C_p} = {10^{ - 10}}{F^2}$;

Step 3: The value of capacitance of a $4\mu F$ capacitor if a dielectric of dielectric constant 2 is inserted fully between the plates of parallel plate capacitor:
$C = \dfrac{{K{\varepsilon _o}A}}{d}$;
Where:
K = Dielectric constant of the material.
A = Area.
d = distance.
${\varepsilon _o}$= Permittivity $8.854 \times {10^{ - 12}}$
Or,
$C' = KC$; … $\left( {C = \dfrac{{{\varepsilon _o}A}}{d}} \right)$
Put in the given value in the above equation and solve:
$\Rightarrow C' = 2 \times 4 = 8\mu F$;

The relation for equivalent capacitance of the series combination of capacitors is $\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}};$ The value of product equivalent capacitances is ${C_s}{C_p} = {10^{ - 10}}{F^2}$; : The value of capacitance of a $4\mu F$ capacitor if a dielectric of dielectric constant 2 is inserted fully between the plates of parallel plate capacitor is $C' = 2 \times 4 = 8\mu F$.

Note: Here we have to explain about the properties of capacitors in series and compare with the capacitors in parallel. Derive the formula for equivalent capacitance in series then solve for the product of equivalent capacitance and find the value of capacitance of $4\mu F$ capacitor if a dielectric of dielectric constant 2 is inserted fully between the plates of parallel plate capacitor.