Question

A: Number of circles passing through (– 2, 1), (– 1, 0), (– 4, 3) is 1.
R: Through three non collinear points in a plane only one circle can be drawn.
(a) Both A and R are individually true and R is the correct explanation of A.
(b) Both A and R are individually true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.

Answer 1

Hint: Check if given points are collinear or not by constructing a line through them. No circle can pass through 3 collinear points.

Complete step-by-step answer:
A: Here we are given three points (– 2, 1), (– 1, 0), (– 4, 3). We have to find whether the number of circles passing through these points is 1 or not.
First of all, we will check if points (– 2, 1), (– 1, 0) and (– 4, 3) are collinear or not.
For that, first we construct a line passing through any two given points say (– 2, 1) and (– 1, 0) and then satisfy the third point in the given line. If the third point that is (– 4, 3) will satisfy the equation of line, then all three points would be collinear as that will mean all points lie on a single line.
We know that line passing through two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is:
$\Rightarrow \left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$
Here, $m=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}$
Therefore, line passing through (– 2, 1) and (– 1, 0) is:
$\Rightarrow \left( y-1 \right)=m\left( x-\left( -2 \right) \right)$
Also, $m=\dfrac{\left( 0-1 \right)}{\left[ -1-\left( -2 \right) \right]}=\dfrac{-1}{-1+2}=\dfrac{-1}{1}=-1$
Here we get, equation of line = (y – 1) = – 1(x + 2)
$\Rightarrow y-1=-x-2$
$L:\Rightarrow x+y+1=0$
Putting third point (– 4, 3) in equation of line, we get,
$L:\left( x+y+1 \right)=0$
$L:\left( -4 \right)+3+1$
$L:-1+1=0$
As, (– 4, 3) also satisfies the equation of line, that means (– 2, 1), (– 1, 0) and (– 4, 3) lies on the same line.

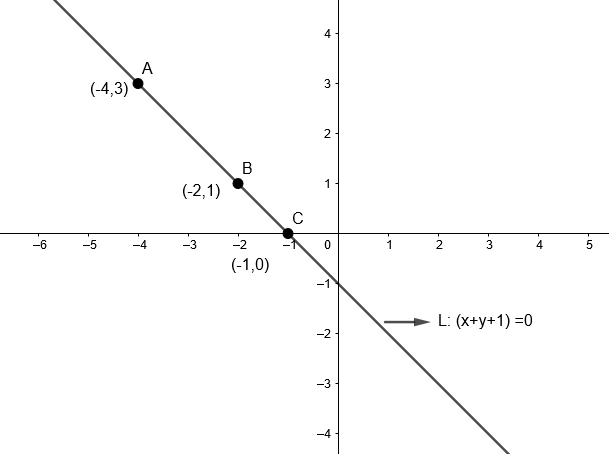
As all three points are collinear, therefore only a line can pass through them. Hence no circle can pass through all three points. Therefore, A is false.
R: Here we have to check if a circle passing through three non collinear points in a plane is one or not.
Let us take three points say A, B and C which are non collinear.

Here, join AB and AC.

First of all, draw the perpendicular bisectors of sides AB and BC.

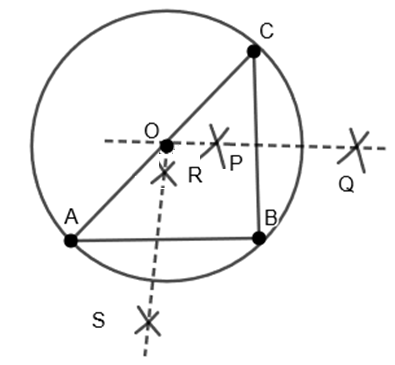
To draw the perpendicular bisector of AB, we have to follow following steps:
1. With A as a center and radius greater than half of AB, draw two arcs above and below AB.
2. Now, with B as center and same radius, draw two arcs cutting the previous arcs and name the points R and S.
3. Join R and S. Hence RS is a perpendicular bisector of AB.
Now to draw the perpendicular bisector of BC, we have to follow following steps:
1. With B as center and radius greater than half of BC, draw two arcs above and below BC.
2. Now with C as center and same radius, draw two arcs cutting previous arcs and name the points P and Q.
3. Join P and Q. Hence PQ is a perpendicular bisector of BC.
Now extend PQ and RS and name their meeting point as O.
As we know that O lies on the perpendicular bisector of AB, therefore we get $OA=OB....\left( i \right)$.
Also, we know that O lies on the perpendicular bisector of BC. Therefore, we get $OB=OC...\left( ii \right)$
From equation (i) and (ii), we get,
$OA=OB=OC=r\text{ (say)}$
Now taking O as center, draw a circle of radius r. This circle will pass through A, B and C points.
As two different lines can meet at one point only that is O [center of circle formed], therefore one and only one circle can pass through three non-collinear points. Hence R is true.
Therefore, A is false but R is true.
Hence, option (d) is the right answer.

Note: We can also check if three points are collinear by equating area of triangle formed by three points which is $\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right|=0$ because no triangle can pass through three collinear points.