Question

A number of 24 ohms resistors are connected as shown in figure. Then the effective resistance between P and Q is

(A) $21.6\Omega$
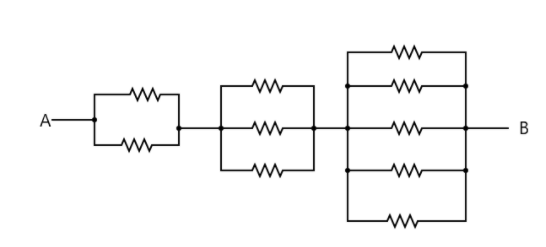
(B) $24.8\Omega$
(C) $26\Omega$
(D) $36\Omega$

Answer 1

The two resistors on the left are parallel to each other, and similarly, the three resistors in the middle and the five resistors at the end are also separately parallel to each other. These equivalent resistances of each of the parallel resistance networks are in series to each other.
Formula used: In this solution we will be using the following formulae;
${R_{eqs}} = {R_1} + {R_2} + ... + {R_n}$ where ${R_{eqs}}$ is the equivalent resistance of resistors connected in series, and ${R_1}...{R_n}$ are the individual resistors in series.
$\dfrac{1}{{{R_{eqp}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}$ where ${R_{eqp}}$ is the equivalent resistance of resistors in a parallel arrangement, and ${R_1}...{R_n}$ are the individual resistors in parallel.

Complete Step-by-Step solution:
From the diagram, we see that the two leftmost resistors are in series to one another, hence, we combine these resistors using the parallel combination formula. The equivalent resistance of resistances in parallel is given by
$\dfrac{1}{{{R_{eqp}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}$ where ${R_1}...{R_n}$ are the individual resistors in parallel.
For the two resistances, we have
$\dfrac{1}{{{R_{eqp}}}} = \dfrac{1}{{24}} + \dfrac{1}{{24}} = \dfrac{2}{{24}}$ (recall from question that all the resistances are 24 ohms)
$\Rightarrow {R_{eqs1}} = 12\Omega$
Similarly, the three resistance of in the middle, are also in series, hence,
$\dfrac{1}{{{R_{eqp2}}}} = \dfrac{1}{{24}} + \dfrac{1}{{24}} + \dfrac{1}{{24}} = \dfrac{3}{{24}}$
$\Rightarrow {R_{eqs2}} = 8\Omega$
Similarly for the rightmost arrangement of 5 parallel resistances, we have $\dfrac{1}{{{R_{eqp2}}}} = \dfrac{1}{{24}} + \dfrac{1}{{24}} + \dfrac{1}{{24}} + \dfrac{1}{{24}} + \dfrac{1}{{24}} = \dfrac{5}{{24}}$
$\Rightarrow {R_{eqs3}} = \dfrac{{24}}{5} = 4.8\Omega$
Now, each of the equivalent parallel resistances are actually in series with each other. The equivalent resistance of resistances in series can be given as
${R_{eqs}} = {R_1} + {R_2} + ... + {R_n}$ where ${R_{eqs}}$ is the equivalent resistance of resistors connected in series, and ${R_1}...{R_n}$ are the individual resistors in series.
Hence, we have
${R_{eqs}} = 12 + 8 + 4.8 = 24.8\Omega$

Hence, the correct option is B

Note: For understanding, resistors are said to be in series if current moving through one of them is equal to the current flowing through the others. Resistors are in parallel if the voltage across each of them are equal to the other.