Question

A normal chord of ${{y}^{2}}=4ax$ subtends an angle $\dfrac{\pi }{2}$ at the vertex of the parabola. If its slope is m, then find the value of $\left( {{m}^{2}}+3 \right)$.

Answer 1

Hint: Suppose two points of the normal chord lying on parabola as $\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $\left( at_{2}^{2},2a{{t}_{2}} \right)$. Let the slope of the tangent at the point where the chord acting as a normal for parabola, by differentiating the curve, ${{y}^{2}}=4ax$ at that point. Hence, get the slope of normal using relation.

Complete step-by-step answer:
Product of slopes of two perpendicular lines = -1.
Get the slope of chord using the coordinates supposed as well with the help of relation $=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are lying on the line. And use the given condition to solve the problem further.

Here, we need to find the value of $\left( {{m}^{2}}+3 \right)$where m is the slope of the normal chord. So, first of all let us find the value of m.
As, we need to find the slope of a chord in ${{y}^{2}}=4ax$, which is normal at one end and subtends a right angle at the origin as well. So, let the two ends of the chord are $\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $\left( at_{2}^{2},2a{{t}_{2}} \right)$. [Parametric coordinates for ${{y}^{2}}=4ax$].
So, diagram can be represented as,

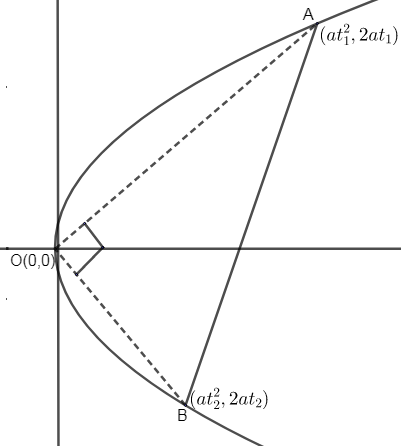
Let AB is acting as a normal at the point B.
We know the slope of tangent at point B can be given as,
${{\left. \dfrac{dy}{dx} \right|}_{\left( at_{2}^{2},2a{{t}_{2}} \right)}}-(i)$
Where, we need to use relation, ${{y}^{2}}=4ax$.
So, differentiating ${{y}^{2}}=4ax$, we get,

& \dfrac{d}{dx}{{y}^{2}}=\dfrac{d}{dx}\left( 4a.x \right) \\\ & 2y\dfrac{dy}{dx}=4a\times 1 \\\ \end{aligned}$$ Where, we know, $$\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}$$ Hence, we get, $$\begin{aligned} & y\dfrac{dy}{dx}=2a \\\ & \dfrac{dy}{dx}=\dfrac{2a}{y} \\\ \end{aligned}$$ Now, we can get slope of tangent at point B as, $${{\left. \dfrac{dy}{dx} \right|}_{\left( at_{2}^{2},2a{{t}_{2}} \right)}}=\dfrac{2a}{2a{{t}_{2}}}=\dfrac{1}{{{t}_{2}}}-(ii)$$ Now, we know tangent is perpendicular to the normal at the point of tangency for any conic. And as, we know the relation between slope of two perpendicular lines is given as, Product of two perpendicular lines = -1 – (iii) So, we get, Slope of normal at B $$\times $$ Slope of tangent at B = -1 $$\dfrac{1}{{{t}_{2}}}\times $$ slope of normal at B = -1 Slope of normal at B = $$-{{t}_{2}}$$ Now, we can calculate slope of normal at B i.e. slope of line AB by formula, Slope = $$\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}-(iv)$$ So, we get, Slope of normal at B $$=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}}$$ $$\begin{aligned} & =\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( t_{2}^{2}-t_{1}^{2} \right)} \\\ & =\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}+{{t}_{1}} \right)\left( {{t}_{2}}-{{t}_{1}} \right)} \\\ \end{aligned}$$ Slope of normal at B = $$\dfrac{2}{\left( {{t}_{2}}+{{t}_{1}} \right)}$$ As, we have already calculated the slope of normal at point B as $$-{{t}_{2}}$$. So, we get, $$\dfrac{2}{{{t}_{1}}+{{t}_{2}}}=-{{t}_{2}}$$ $$\begin{aligned} & -2={{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \\\ & {{t}_{1}}{{t}_{2}}+t_{2}^{2}=-2-(v) \\\ \end{aligned}$$ Now, as AO and BO are perpendicular to each other. So, we can calculate the slopes of them and use equation (iii). So, we get slope of AO from the equation (iv) as, Slope of AO = $$\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}=\dfrac{2a{{t}_{1}}}{at_{1}^{2}}$$ Slope of AO $$=\dfrac{2}{{{t}_{1}}}$$ Similarly, slope of BO $$=\dfrac{2}{{{t}_{2}}}$$ Now, using equation (iii), we get, $$\begin{aligned} & \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\\ & 4=-{{t}_{1}}{{t}_{2}} \\\ \end{aligned}$$ Or $${{t}_{1}}{{t}_{2}}=-4-(vi)$$ Now, putting, $${{t}_{1}}{{t}_{2}}=-4$$ to the equation (v), we get, $$\begin{aligned} & -4+t_{2}^{2}=-2 \\\ & t_{2}^{2}=4-2=2 \\\ & {{t}_{2}}=\pm \sqrt{2} \\\ \end{aligned}$$ We know the slope of the chord is given as $$-{{t}_{2}}$$. So, the possible slope of the chord is $$\pm \sqrt{2}$$. So, we get, $$m=\pm \sqrt{2}$$ Hence, value $$\left( {{m}^{2}}+3 \right)$$ can be given as, $${{\left( \pm \sqrt{2} \right)}^{2}}+3=2+3=5$$ So, 5 is the answer to the problem. Note: One may get confused with the two values of slopes i.e. $$\pm \sqrt{2}$$. It is because angles formed with the x – axis can be given as $$\theta $$ and $$180-\theta $$ both. So, one will give positive when, $$\left( 0<\theta <{{90}^{\circ }} \right)$$ and another will give negative, for $$90<\theta <{{180}^{\circ }}$$. Hence, be clear with this step in the solution as well. We can use another approach to get the slope of the normal at any conic as well. We can write the equation of tangent at point A and B by using equation, T = 0. i.e. replace $${{x}^{2}}$$ by $$x{{x}_{1}}$$, $${{y}^{2}}$$ by $$y{{y}_{1}}$$. x by $$\dfrac{x+{{x}_{1}}}{2}$$, y by $$\dfrac{y+{{y}_{1}}}{2}$$, where $$\left( {{x}_{1}},{{y}_{1}} \right)$$ is the point on the given sonic. Hence, compare the calculated equation of tangent with the line $$y=mx+c$$ to get slope of tangent and hence, get slope of normal by relation. Product of slopes of two perpendicular lines = -1 One may directly use the result $${{t}_{1}}{{t}_{2}}=-4$$ for parabola $${{y}^{2}}=4ax$$, if any chord is subtending an angle of $${{90}^{\circ }}$$at the vertex of the parabola. It can be used for future reference for the given condition in the problem. It will make the solution more flexible and less time taking.