Question
Question: A normal chord of the parabola \[{{y}^{2}}=4x\] subtending a right angle at the vertex makes an acut...
A normal chord of the parabola y2=4x subtending a right angle at the vertex makes an acute angle θ with the x –axis, then θ is
(a)tan−12
(b)sec−1(3)
(c)cot−1(3)
(d)None
Solution
Hint: Use the property of two perpendicular lines with respect to slopes of them.
Product of slopes of two perpendicular lines = -1.
Complete step-by-step answer:
Suppose two points of the normal chord lying on parabola as (t12,2t1) and (t22,2t2). Get the slope of the chord by differentiating the curve (Parabola) at the point where normal is drawn. Get the slope of a line using the relation,
m=x2−x1y2−y1, where (x1,y1) and (x2,y2) are the points lying on the line.
As we need to find the angle θ formed (inclination) with the axis of parabola, y2=4ax with the help of given in formations in the problem.
We know the axis of parabola y2=4ax is x – axis, as it is symmetric about x – axis. So, we need to determine the angle with the x – axis. So we can calculate the slope of the chord and equate it to the tanθ because slope is defined as tan of angle formed with the positive direction of x –axis.
So, let us suppose slope of normal chord = tanθ
As, we need to find the slope of a chord of, which is normal at one end and subtends a right angle at the origin as well. So, let the two ends of the chord are (t12,2t1) and (t22,2t2). [Parametric coordinates for y2=4ax is given as at2,2at].
So, diagram can be represented as,
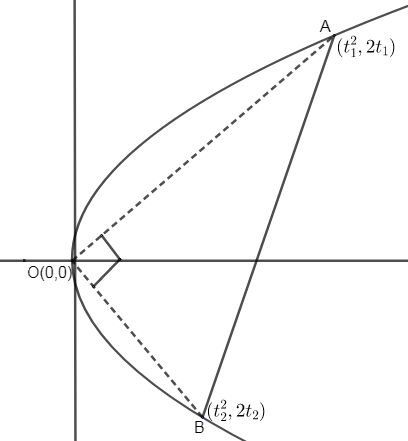
Let AB is acting as a normal at the point B.
We know the slope of tangent at point B can be given as,
dxdy(at22,2at2)−(i)
Where, we need to use relation, y2=4x.
So, differentiating, y2=4x, we get,
