Question

A non-viscous liquid of density $d$ is filled in a cylinder up to a height ${h_0}$ . A hole is then made on the side of the cylinder at a height ${h_1}$ from the bottom of the cylinder. Find the velocity of the liquid coming out of the hole.
A) $v = \sqrt {2g{h_0}}$
B) $v = \sqrt {2g\left( {{h_0} - {h_1}} \right)}$
C) $v = \sqrt {dg{h_1}}$
D) $v = \sqrt {dg{h_0}}$

Answer 1

The flow rate or volume flux will be the same at the top of the container and at the hole, i.e., $Av$ is a constant throughout the flow of the liquid out of the hole.

Formulas used:
-Equation of continuity gives us, $Av = {\text{constant}}$ throughout the flow where $Av$ is the flow or volume flux rate of the liquid.
-Bernoulli’s equation gives us, $P + \dfrac{1}{2}d{v^2} + dgh = {\text{constant}}$ , where $P$ is the pressure, $\dfrac{1}{2}d{v^2}$ is the kinetic energy per unit volume and $dgh$ is the potential energy per unit volume.

Complete step by step answer.
Step 1: Sketch a diagram to represent the different parameters involved in the problem.

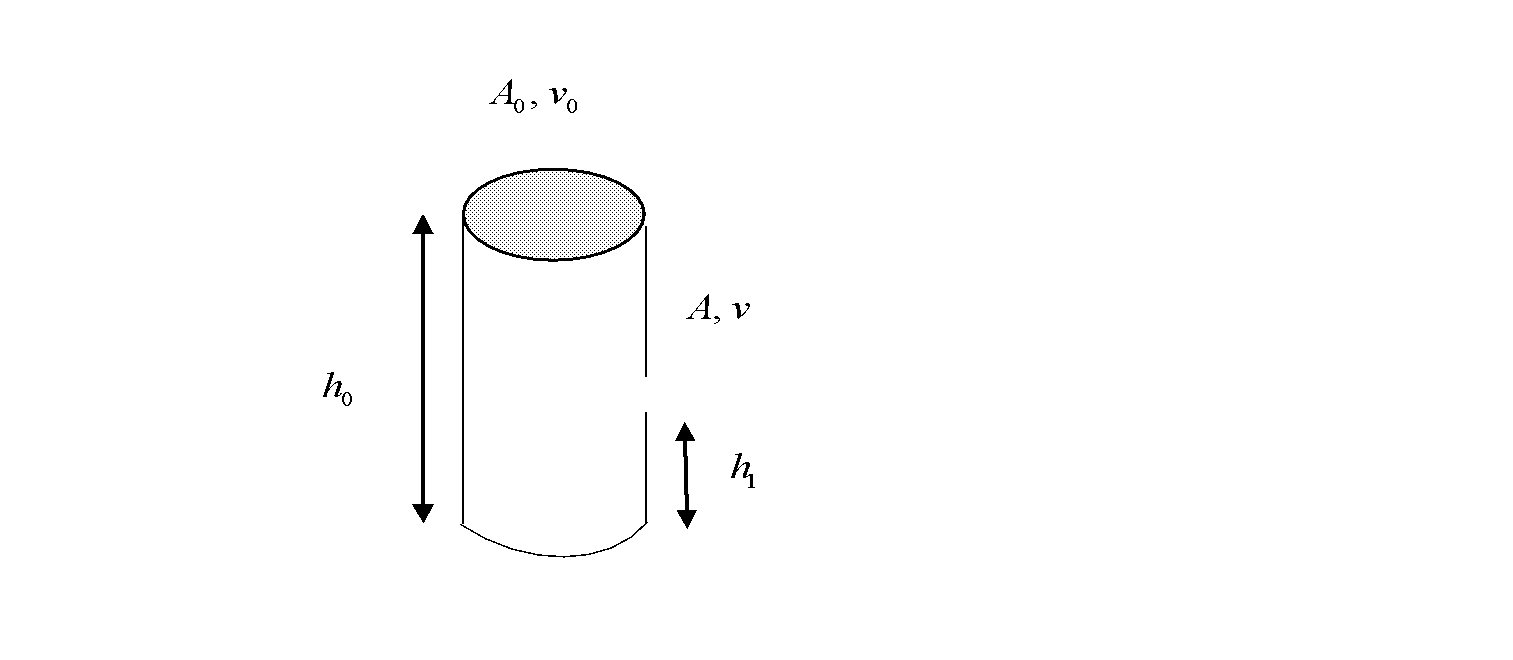
Let ${A_0}$ be the area of the cross-section at the top of the container and $A$ be the area of the cross-section at the hole of the container. The density of the liquid that is filled in the cylinder is $d$ .
The hole is made at a height ${h_1}$ from the bottom of the cylinder in which liquid is filled up to a height ${h_0}$ .
The velocities of the liquid at the top of the container and at the hole are represented respectively by ${v_0}$ and $v$ .
At the top of the cylinder, the pressure of the air existing above the liquid is $P$ .
Step 2: Using the equation of continuity and Bernoulli’s principle, find the expression for the velocity of the liquid flowing out of the hole.
Equation of continuity states that the volume flux remains constant throughout the flow.
Hence, ${A_0}{v_0} = Av$ where, ${A_0}{v_0}$ is the volume flux at the top of the cylinder and $Av$ is the volume flux at the hole.
Applying Bernoulli’s principle at the top of the surface of the liquid and at the hole we get, $P + \dfrac{1}{2}d{v_0}^2 + dg{h_0} = {P_1} + \dfrac{1}{2}d{v^2} + dg{h_1}$ --------- (1)
At the top of the cylinder, the velocity is zero i.e., ${v_0} = 0$
Now equation (1) becomes, $P + dg{h_0} = {P_1} + \dfrac{1}{2}d{v^2} + dg{h_1}$
On simplifying the above equation we get, $2P + 2dg{h_0} = 2{P_1} + d{v^2} + 2dg{h_1}$
Then, ${v^2} = \dfrac{{2\left( {P - {P_1}} \right)}}{d} + 2g\left( {{h_0} - {h_1}} \right)$
Taking the square root we get, $v = \sqrt {2g\left( {{h_0} - {h_1}} \right) + \dfrac{{2\left( {P - {P_1}} \right)}}{d}}$ ------ (2)
Since the cylinder and the hole are open to the atmosphere, the pressure of the air at the liquid surface and at the hole will be the atmospheric pressure, i.e., $P = {P_1} = {P_a}$ .
Now equation (2) becomes $v = \sqrt {2g\left( {{h_0} - {h_1}} \right)}$

Therefore, the velocity of the liquid coming out of the hole is $v = \sqrt {2g\left( {{h_0} - {h_1}} \right)}$ .

Note: The area of cross-section of the cylinder at the top will be much greater than the area of the hole on the side of the cylinder i.e, ${A_0} > > A$. So, we assume that at the top of the cylinder, the velocity ${v_0}$ of the liquid is zero as ${A_0}{v_0} = Av$ .