Solveeit Logo
Login

Question

Question: A non-viscous liquid of constant density \[1000kg/{{m}^{3}}\] flows in a streamline motion along a t...

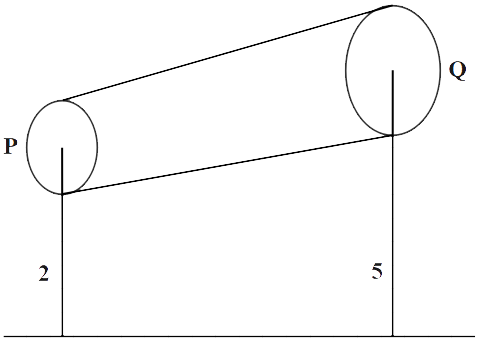
A non-viscous liquid of constant density 1000kg/m31000kg/{{m}^{3}} flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in a vertical plane as shown in the figure. The area of cross section of tube at two points P and Q at heights of 2m and 5m are respectively 4×10−3m24\times {{10}^{-3}}{{m}^{2}} and A2=8×10−3m2{{A}_{2}}=8\times {{10}^{-3}}{{m}^{2}} . The velocity of liquid at point P is 1 m/s. Find the work done per unit volume by the pressure and the gravity forces as the liquid flows from point P to Q. Take g=9.8m/s2g=9.8m/{{s}^{2}}

Explanation

Solution

To solve this question we will need the pressure across the points as the liquid flows from point P to point Q. To do that, we will first find velocity at point Q as it is not given and then using this value find the pressure across points P and Q. To find the pressure and work done by it we will use Bernoulli’s equation. To find the work done by gravity we will use the equation of potential energy between the given points.
Formula used:
A1v1=A2v2{{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}
p1+12ρv12+ρgh1=p2+12ρv22+ρgh2{{p}_{1}}+\dfrac{1}{2}\rho v_{1}^{2}+\rho g{{h}_{1}}={{p}_{2}}+\dfrac{1}{2}\rho v_{2}^{2}+\rho g{{h}_{2}}

Complete answer:
Let W1{{W}_{1}} = work done by pressure and W2{{W}_{2}}= work done by gravity.
To solve this problem we will first need to find the velocity at point Q
So, using the given data
A1=4×10−3m2{{A}_{1}}=4\times {{10}^{-3}}{{m}^{2}}
A2=8×10−3m2{{A}_{2}}=8\times {{10}^{-3}}{{m}^{2}}
ρ=103kg/m3\rho ={{10}^{3}}kg/{{m}^{3}}
v1{{v}_{1}}= 1 m/s
Now using equation of continuity
A1v1=A2v2{{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}
We get,
v2=(A1A2)v1{{v}_{2}}=\left( \dfrac{{{A}_{1}}}{{{A}_{2}}} \right){{v}_{1}}
Substituting the given values,
We get,
v2=(4×10−34×10−3)×1{{v}_{2}}=\left( \dfrac{4\times {{10}^{-3}}}{4\times {{10}^{-3}}} \right)\times 1
∴v2=12m/s\therefore {{v}_{2}}=\dfrac{1}{2}m/s …….. (1)
Now, using Bernoulli’s equation to find work done by pressure
p1+12ρv12+ρgh1=p2+12ρv22+ρgh2{{p}_{1}}+\dfrac{1}{2}\rho v_{1}^{2}+\rho g{{h}_{1}}={{p}_{2}}+\dfrac{1}{2}\rho v_{2}^{2}+\rho g{{h}_{2}}
On rearranging the terms,
p1−p2=ρg(h2−h1)+12ρ(v22−v12){{p}_{1}}-{{p}_{2}}=\rho g\left( {{h}_{2}}-{{h}_{1}} \right)+\dfrac{1}{2}\rho \left( v_{2}^{2}-v_{1}^{2} \right) ………….. (2)
We get the Work energy principle.
Therefore,
W1=p1−p2{{W}_{1}}={{p}_{1}}-{{p}_{2}}

So from (1) and (2)
We get,
W1{{W}_{1}}=p1−p2=[(103)(9.8)(5−2)+12(103)(14−1)]{{p}_{1}}-{{p}_{2}}=\left[ \left( {{10}^{3}} \right)\left( 9.8 \right)\left( 5-2 \right)+\dfrac{1}{2}\left( {{10}^{3}} \right)\left( \dfrac{1}{4}-1 \right) \right]
∴p1−p2=29025J/m3\therefore {{p}_{1}}-{{p}_{2}}=29025J/{{m}^{3}}
Therefore, work done by pressure is W1{{W}_{1}}=29025J/m329025J/{{m}^{3}}

Now, for work done by gravity we shall use the equation of potential energy
W2=ρg(h2−h1){{W}_{2}}=\rho g\left( {{h}_{2}}-{{h}_{1}} \right)
Substituting the values
We get,
W2=(103)(9.8)(5−2){{W}_{2}}=\left( {{10}^{3}} \right)\left( 9.8 \right)\left( 5-2 \right)
W2=29400J/m3{{W}_{2}}=29400J/{{m}^{3}}
Therefore, the work done by gravity is W2=29400J/m3{{W}_{2}}=29400J/{{m}^{3}}

Note:
We have used Bernoulli's equation to find the net work done because as the fluid flows from a narrow channel to a broad one the kinetic energy of fluid increases and vice versa. This change in kinetic energy occurs due to net work done on the fluid to push it further in a channel and work done by gravitational force, if there is change in vertical position of fluid.