Question

A non-uniform thin rod of length L is placed along $x$-axis as such its one of ends at the origin. The linear mass density of rod is $\lambda ={{\lambda }_{0}}x$. The distance of centre of mass of rod from the origin is:
(A) L/2
(B) 2L/3
(C) L/4
(D) L/5

Answer 1

We have formulae for centre of mass of various solid and standard figures (for example, we know that the centre of mass of a rod is at its mid-point) but that is only if the object given to us has uniform mass distribution, but in this case our mass distribution is non-uniform, so we’ll use the integration approach.

Complete step by step answer:

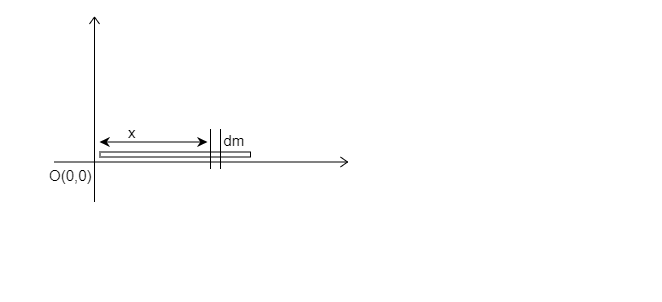
- The first step to an integration approach (for non-uniform mass distributed objects) is to consider a differential mass particle in our object at a certain position, say $x$. In this question for instance, one end of our rod is at origin, so we’ll consider a differential mass $dm$ of length $dx$ at $x$ distance from the origin.
- Since the linear mass density of the rod is given to us, we can find our differential mass. Here, mass $dm={{\lambda }_{0}}xdx$.
- Now, we can use the following expression to find the centre of mass for non-uniform mass distributed objects.
${{X}_{CM}}=\dfrac{\int\limits_{0}^{L}{xdm}}{\int\limits_{0}^{L}{dm}}$
Substituting the values, we get ${{X}_{CM}}=\dfrac{\int\limits_{0}^{L}{{{\lambda}_{0}}{{x}^{2}}dx}}{\int\limits_{0}^{L}{{{\lambda}_{0}}xdx}}$=$${{X}{CM}}=\dfrac{{{\lambda}{0}}\left[\dfrac{{{x}^{3}}}{3}\right]{0}^{L}}{{{\lambda}{0}}\left[\dfrac{{{x}^{2}}}{2}\right]_{0}^{L}}$$$=\dfrac{\dfrac{{{L}^{3}}}{3}}{\dfrac{{{L}^{2}}}{2}}=\dfrac{2L}{3}$

Note: You must be wondering why we are using a differential mass. We use a differential mass because we can consider it as a point object and hence apply equations of physics meant for point objects on a solid body.
We also came across the term linear mass density in our question. Linear mass density is simply the mass of a unit length of the given object. Similarly we have surface mass density and volume mass density which stand for the mass of a unit area of an object and the mass of a unit volume of an object respectively.
So if the mass of a unit length of the object is given to us, we can easily find the mass of any portion of the object simply by multiplying the length of that portion with the linear mass density.