Question

A non-uniform rod $AB$ has a mass and length $2l$ the mass per unit length of the rod is $mx$ at a point of rod distant $x$ from. Find the moment of inertia of this rod about an perpendicular to the rod (a) through $A$ (b) through the midpoint of $AB$

Answer 1

Here they have given the mass of the rod $M$ and they also given the length of the rod that is $2l$ here in the question they have mentioned that mass per unit length of rod = $mx$ of a point distance $x$ from $A$
We have to find the moment of inertia of this rod about a perpendicular axis (a) through $A$ (b) through the midpoint of $AB$

Complete step by step solution:

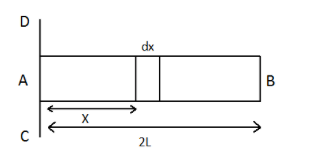
Given that the mass of the rod is $M$ and the length of the rod that is $2l$
Consider the small mass of a length $dx$ and mass $dm$ from the point $A$, then the mass per unit length can be given as:
$dM = {\text{ }}mxdx$

On integrating the above equation we will get total mass of rod on LHS and RHS can be integrated from $x = 0$to $x = 2l.$Then the Equation becomes,

$\int {dM} = {\text{ }}\int\limits_0^{2l} {mxdx}$

After integrating the above equation we get

$M = m\left[ {\dfrac{{{x^2}}}{2}} \right]_0^{2l}$

Now apply the limit to the above equation

$M = m\left[ {\dfrac{{{{(2l)}^2}}}{2}} \right]$

Then after further simplifying the above equation we get

$M{\text{ }} = {\text{ }}2m{l^2}$

Now take $m$ outside then the equation becomes

$m = \dfrac{M}{{2{l^2}}}..........(1)$

Now the moment of inertia of rod is given by

$dI{\text{ }} = {\text{ }}mx{x^2}dx$

For the inertia at $A$, we have to integrate from $0$to $2l$

$I = \int\limits_0^{2l} {m{x^3}} dx$

After integrating we get

$I = m\left[ {\dfrac{{{x^4}}}{4}} \right]_0^{2l}$

After applying limits we get

$I = 4m{l^4}$

Now substitute the value of $m$from equation $(1)$so we get

$I = 4\left( {\dfrac{M}{{2{l^2}}}} \right){l^4}$

After simplifying above equation we get

$I = 2M{l^2}$

For part B

Consider the midpoint as a origin and the length of the rod is from $- L$ to $+ L$ and element of mass is $dm$and length $dx$at $\left( {L - x} \right)$

Now the Mass of the element is given as

$dM = {\text{ }}m\left( {L - x} \right)dx$

Now the Moment of inertia of the rod can be taken as

$dI = {\text{ }}m\left( {L - x} \right){x^2}{\text{ }}dx.$

Now integrate the above equation for the limits $- L$ to $+ L$ we get

$I = \int\limits_{ - L}^{ + L} {\left( {L{x^2} - {x^3}} \right)} dx$

After integrating the above equation we get

$I = \left( {\dfrac{{L{x^3}}}{3} - \dfrac{{{x^4}}}{4}} \right)_{ - L}^{ + L}$

Now apply the limits

$I = m\left[ {\left( {\dfrac{{{L^4}}}{3} - \dfrac{{{L^4}}}{4}} \right) - \left( { - \dfrac{{{L^4}}}{3} - \dfrac{{{L^4}}}{4}} \right)} \right]$

We have to substitute the value of m from (1) and after simplifying we get

$I = \dfrac{{M{L^3}}}{3}$

Note: The Moment of inertia is defined as the quantity expressed by the body resisting an angular acceleration which is the sum of the product of mass of every particle.