Question

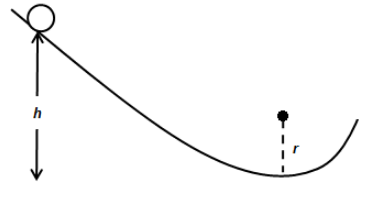
A non uniform ball of mass M and radius R, rolls from a rest down a ramp and onto a circular loop of radius r. The ball is initially at height h above the bottom of the loop. At the bottom of the loop the normal force on the ball is twice its weight. Moment of inertia of the ball is given by $I = \beta M{R^2}$. Find $\beta$.
(Assume $h \gg R$ and $r \gg R$)

A. $\dfrac{h}{R}$
B. $\dfrac{{2h}}{r}$
C. $\dfrac{{2h}}{r} - 1$
D. $\dfrac{{2h}}{r} + 1$

Answer 1

As the ball rolls down a ramp from height h to the bottom of the loop, the loss in the potential energy will be used to increase the kinetic energy of the ball. Using this, express the potential energy of the ball at the top position. Determine the forces acting on the ball at the bottom of the loop using Newton’s second law of motion. Solving these two equations, you will get the value of $\beta$.

Formula used:
Potential energy, $U = Mgh$,
where, M is the mass, g is the acceleration and h is the height.
Kinetic energy, $K = \dfrac{1}{2}m{v^2}$,
where, v is the velocity.
Rotational kinetic energy, $K = \dfrac{1}{2}I{\omega ^2}$,
where, I is the moment of inertia and $\omega$ is the angular velocity.
Centrifugal force or centripetal force, ${F_C} = \dfrac{{m{v^2}}}{r}$,
where, r is the radius of the circular motion

Complete step by step answer:
As the ball rolls down a ramp from height h to the bottom of the loop, the loss in the potential energy will be used to increase the kinetic energy of the ball. We know that for the rolling and translational motion, the kinetic energy is the contribution of translational kinetic energy and rotational kinetic energy. Let us apply the law of conservation of energy as follows,
$Mgh = \dfrac{1}{2}M{v^2} + \dfrac{1}{2}I{\omega ^2}$ …… (1)
Here, g is the acceleration due to gravity, h is the height, v is the linear velocity of the ball at the bottom, I is the moment of inertia of the ball and $\omega$ is the angular velocity of the ball.

We know the relation,
$v = R\omega$
$\Rightarrow \omega = \dfrac{v}{R}$
Using the above equation in equation (1), we get,
$Mgh = \dfrac{1}{2}M{v^2} + \dfrac{1}{2}I{\left( {\dfrac{v}{R}} \right)^2}$
We have given that the moment of inertia of the ball is $I = \beta M{R^2}$. Therefore, the above equation becomes,
$Mgh = \dfrac{1}{2}M{v^2} + \dfrac{1}{2}\left( {\beta M{R^2}} \right){\left( {\dfrac{v}{R}} \right)^2}$
$\Rightarrow Mgh = \dfrac{1}{2}M{v^2} + \dfrac{1}{2}\beta M{v^2}$
$\Rightarrow Mgh = \dfrac{1}{2}M{v^2}\left( {1 + \beta } \right)$ …… (2)

Now, let us draw the free body diagram of the forces acting on the ball at the bottom position as follows,

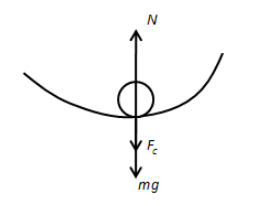
From the above figure, we can write,
$N - mg - {F_C} = 0$
$\Rightarrow N - mg = {F_C}$
$\Rightarrow N - mg = \dfrac{{M{v^2}}}{r}$
We have given that the normal force at the bottom is twice the weight of the ball. Therefore, we can write,
$2mg - mg = \dfrac{{M{v^2}}}{r}$
$\Rightarrow mg = \dfrac{{M{v^2}}}{R}$
Using the above equation in equation (2), we get,
$\left( {\dfrac{{M{v^2}}}{r}} \right)h = \dfrac{1}{2}M{v^2}\left( {1 + \beta } \right)$
$\Rightarrow \dfrac{h}{r} = \dfrac{1}{2}\left( {1 + \beta } \right)$
$\therefore \beta = \dfrac{{2h}}{r} - 1$

So, the correct answer is option C.

Note: In the formula for centripetal force, r is the radius of the circular motion and not the radius of the ball. The direction of the centrifugal force is always away from the centre of the circular motion. From the free body diagram, we have balanced forces using Newton’s second law and the acceleration of the ball in the vertical direction is zero.