Question
Question: A non-relativistic charged particle flies through the electric field of a cylindrical capacitor and ...
A non-relativistic charged particle flies through the electric field of a cylindrical capacitor and gets into a uniform transverse magnetic field with induction B. In the capacitor the particle moves along the arc of a circle, in the magnetic field, along a semicircle of radius r. The potential difference applied to the capacitor is equal to V, the radii of the electrodes are equal to a and b, with a<b. Find the velocity of the particle and its specific charge q/m.
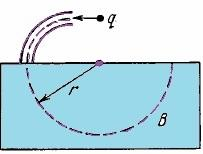
Solution
This is a problem of cylindrical capacitor. Break the question into segments and then solve. Write the formula for electric potential and field for a cylindrical capacitor. Then apply the concept of centripetal and magnetic force on a charge along with the magnetic field and form a relation between the three.
Complete step by step solution:
Step 1: Write the formula electric field and potential for a cylindrical capacitor.
The potential is given as:
ΔV=−E.dr;
Take integration on both the sides:
∫ΔV=−a∫bE.dr;
∫ΔV=−a∫b2πεorλ.dr; ….(Here: E=2πεorλ)
Take the constants out of the integration:
∫ΔV=−2πεoλa∫br1.dr;
Solve the integration by applying the integration property:∫r1dr=lnr
V=−2πεoλ[lnr]ab;
Apply the logarithmic property: [lnr]ab=[lnb−lna], in the above equation
V=−2πεoλ[lnb−lna];
Here, [lnb−lna]=lnab:
V=−2πεoλlnab;
The Electric field is given as:
E=2πεorλ;
E.r=2πεoλ;
Put E in place of 2πεoλ in the equation for electric potential:
V=−E.rlnab;
Write the above equation in terms of electric potential;
E=rlnab−V;
Step 2: Now, we know the magnetic force on a charge particle:
F=q.(v×B);
We also know the centripetal force on a charge in a magnetic field
Fc=rmv2;
Here the magnetic force supplies the centripetal force, so we can equate them together:
q.(v×B)=rmv2;
Now, electric field is equal to:
E=(v×B);
Put the above relation in the equation between centripetal and magnetic force:
q.E=rmv2;
Put the value of the electric field E=rlnabV. In the above relation
q.rlnabV=rmv2;
Cancel out the common;
mv2=q.ln(b/a)V;
We have already established that the centripetal force Fc=rmv2 is equal to the magnetic force Fm=qvb:
rmv2=qvB;
Cancel out the common variable;
rmv=qB;
Take “r” to RHS we have:
mv=qBr;
Put this relation in the equation mv2=q.ln(b/a)V:
(qBr).v=q.ln(b/a)V;
Cancel out the common variable on both the sides:
(Br).v=ln(b/a)V;
Solve for the velocity,
v=Brln(b/a)V;
v=Brln(b/a)V;
Step 3: Find specific charge (q/m).
We know that:
mv=qBr;
Write the above equation in terms of q/m.
mq=vBr;
Put the value of v=Brln(b/a)V in the above relation and solve,
mq=Brln(b/a)VBr;
Solve,
mq=Br×Brln(b/a)V;
mq=Br2ln(b/a)V;
The velocity of the particle and its specific charge q/m is v=Brln(b/a)Vand mq=Br2ln(b/a)V.
Note: It is a very lengthy process, be careful while formulating relations and writing the formulas. Go step by step. First write the potential and electric field and establish a relation between them. Then apply centrifugal force and magnetic force and equate them together. Then apply a magnetic field and find out the velocity and then the specific charge.
