Question
Question: A non-planar loop of conducting wire carrying a current \[I\] is placed as shown in the figure. Each...
A non-planar loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at point P(a,0,a) points in the direction
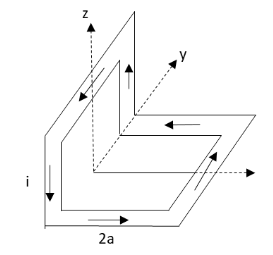
A. 21(−j^+k^)
B. 31(−j^+k^+i^)
C. 31(i^+k^+j^)
D. 21(i^+k^)
Solution
Divide the given non-planar current carrying loop into two loops. Determine the direction of the electric current flowing through these two loops and hence determine the direction of the magnetic field in these loops. From the directions of the magnetic field in these loops, pick the correct answer from the options.
Complete step by step answer:
We have given that an electric current I flows through the non-planar loop of the current carrying conductor. The length of each section of the loop is 2a. We have asked to determine the magnetic field at point P(a,0,a).
Let us first divide the given non-planar loop of current carrying conductor into two loops as follows:
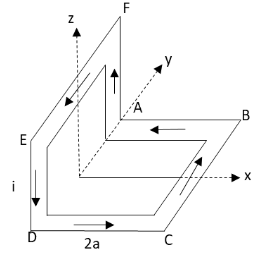
In the above diagram of the non-planar loop, there are two loops ABCDA and AFEDA. In the loop ABCDA, the electric current flows from A to D and in the loop AFEDA, the electric current flows from D to A. The direction of the magnetic field in the loop ABCDA is in the upward direction which is the direction of the Z-axis. Hence, the direction of the magnetic field in this loop is along the direction of the unit vector k.
The direction of the magnetic field in the loop AFEDA is along the direction of the X-axis. Hence, the direction of the magnetic field in this loop is along the direction of the unit vector i. Also, the magnitude of the magnetic field in both of these loops at point is the same. Thus, the resultant magnetic field at the point P(a,0,a) is only in the X and Z direction having unit vectors i^ and k^ respectively which is 21(i^+k^). If we observe the options carefully, there is only one option having the resultant magnetic field at point P in X and Z-direction.
Hence, the correct option is D.
Note: One can also solve the same question by another method. One can use the formula for the magnetic field due to the circular current at the centre of the circular loop. Using this formula one can conclude that the magnetic field due to both the considered loops is the same but in different directions which gives the answer for this question.
