Question

A non-conducting ring of radius ‘ $R$ ’ has a uniformly distributed positive charge $Q$ . A small part of the ring of length $d$ , is removed $(d < < R)$ . The electric field at the centre of the ring will now be:
(A) directed towards the gap, inversely proportional to ${R^3}$
(B) directed towards the gap, inversely proportional to ${R^2}$
(C) directed away from the gap, inversely proportional to ${R^3}$
(D) directed away from the gap, inversely proportional to ${R^2}$

Answer 1

To solve this question, the electric field at the center of the total ring and the electric field due to the small part of the ring should be found. The direction of the electric field lines is directed from the positive charge to the negative charge. So it would help to analyze the direction of the resultant electric field.

Complete answer:
Coulomb’s Law states that the force between two point charges is directly proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them.
$\,\,\,\,\,\,F \propto \dfrac{{{q_1}\,{q_2}}}{{{r^2}}}$
$\Rightarrow F = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{{q_1}\,{q_2}}}{{{r^2}}}$
Where $F =$ force in Newton
${q_1}\,\& \,{q_2} =$ charge in Coulombs
$r =$ distance between two charges in meter
${\varepsilon _o} =$ the permittivity of free space
When a charge is placed in a space and a second charge is brought near it, the second charge will experience an electrostatic force. This space is referred to as the electric field. The electric field at a point due to a point charge is equal to the force experienced by the test unit positive charge placed at that point.
$\,\,\,\,\,\,\,E = \dfrac{F}{q}$
$\Rightarrow E = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{q}{{{r^2}}}$
Where $F =$ force in Newton
$q =$ charge in Coulombs
$r =$ distance between two charges in meter
${\varepsilon _o} =$ the permittivity of free space
Now, the electric field at the center of the total ring is zero due to symmetry and uniformly distributed charged particles. It is given that the charge on the entire ring is $Q$ . According to the question, if we remove a small part of length $d$ from the ring, as shown in the diagram, the electric field developed at the center due to the small part and the remaining part of the ring should be equal and opposite in direction so that the electric field at the center is zero. As the charge is positive in nature, the electric field lines are directed outwards.

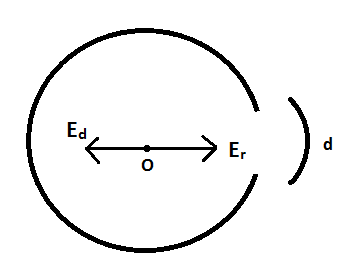
Let the surface charge density of the ring is denoted by $\rho$ . Surface charge density is defined as charge per unit surface area. So, the surface charge density of the ring is given by:
$\rho = \dfrac{Q}{{2\pi R}}$
Where $Q =$ charge on the ring
$R =$ the radius of the ring
A small part of the length $d$ is removed. So charge on this small part is given by:
$\,\,\,\,\,\,dq = \rho .\,d$
$\Rightarrow dq = Q\dfrac{d}{{2\pi R}}$
For the electric field at the center to be zero, ${E_r} = {E_d}$ .
Where ${E_r} =$ Electric field due to the remaining part
${E_d} =$ Electric field due to the small part
So, the electric field due to the small part is:
$\,\,\,\,\,\,{E_d} = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{dq}}{{{R^2}}}$
$\Rightarrow {E_d} = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{\left( {\dfrac{{Q\,d}}{{2\pi R}}} \right)}}{{{R^2}}}$
$\Rightarrow {E_d} = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{Q\,d}}{{2\pi {R^3}}}$
So, from the equation, we can conclude that the electric field is inversely proportional to ${R^3}$ and the electric field is directed towards the gap to balance the fields.
Therefore, option (A) is the correct answer.

Note:
Electric field lines are imaginary lines. It is used to represent the path followed by a unit positive test charge. The idea of field lines was introduced by Michael Faraday. Field lines originate from a positive charge and terminate at a negative charge, thus giving the direction of the field.
These electric field lines never intersect each other because, at the point of intersection, the net intensity will have two different directions which is not possible. Also, inside a conductor, the electric field is zero and hence there are no field lines inside a conductor.