Question

A non conducting ring of radius $R$ and mass $m$ having charge $q$ uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying uniform magnetic field $B = 4{t^2}$ is switched on at time $t = 0$ . The coefficient of friction between the ring and the table, if the ring starts rotating at $t = 2s$ , is:

(A) $\dfrac{{4qmR}}{g}$
(B) $\dfrac{{2qmR}}{g}$
(C) $\dfrac{{8qR}}{{mg}}$
(D) $\dfrac{{qR}}{{2mg}}$

Answer 1

Hint : To solve this question, we need to use the Faraday’s law to find out the induced emf across the circumference of the ring. Then we have to find the electric field with the help of which the torque produced by the electric force can be found. Finally on equating the electric torque at the given time with the maximum frictional torque we will get the required answer.

Formula used: The formulae used to solve this question are given by
$\varphi = BA\cos {{\theta }}$ , here $\varphi$ is the magnetic flux induced on a surface of area $A$ due to a magnetic field $B$ , and ${{\theta }}$ is the angle between the magnetic field and the area vector.
$e = \dfrac{{d\varphi }}{{dt}}$ , here $e$ is the emf induced due to a changing magnetic flux $\varphi$ with the time $t$ .

Complete step by step answer
Let us consider the coefficient of friction to be $\mu$ .
The ring is placed on a horizontal surface, while the magnetic field is vertical. So, the magnetic field is normal to the plane of the ring and hence parallel to its area vector. So the magnetic flux through the ring is given by
$\varphi = BA\cos {0^ \circ }$ …………………………….(1)
According to the question, the radius of the ring is $R$ . So the area is given by
$A = \pi {R^2}$
Also, the magnetic field is given as $B = 4{t^2}$ . Therefore from (1) the magnetic flux through the ring is
$\varphi = \left( {4{t^2}} \right)\left( {\pi {R^2}} \right)\cos {0^ \circ }$
$\Rightarrow \varphi = 4\pi {R^2}{t^2}$ …………………………….(2)
As can be seen above the flux through the ring is a function of time. So it varies with the time. We know that the changing magnetic flux through a surface generates an emf around its circumference. From the Faraday’s law, magnitude of this emf is given by
$e = \dfrac{{d\varphi }}{{dt}}$
From (2)
$e = \dfrac{{d\left( {4\pi {R^2}{t^2}} \right)}}{{dt}}$
$\Rightarrow e = 8\pi {R^2}t$ …………………………….(3)
Now, we know that the electric field is related to the potential difference by
$E = \dfrac{V}{L}$
So the electric field along the circumference of the ring is
$E = \dfrac{e}{{2\pi R}}$
From (3)
$E = \dfrac{{8\pi {R^2}t}}{{2\pi R}}$
$\Rightarrow E = 4Rt$ …………………………….(4)
Now, the ring has a uniform distribution of the charge $q$ over its circumference. So the force on the charges is given by
$F = qE$
From (4)
$F = 4qRt$ …………………………….(5)
We know that the electric force on a positive charge acts in the direction of the electric field. The electric field is present at the circumference of the ring. So the electric force acts tangentially along the whole of the circumference of the ring, as shown in the figure below.

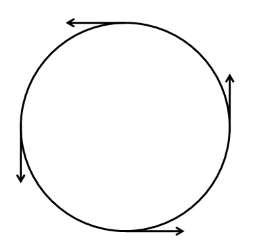
As we can clearly see, the electric forces form couples which produce net torque about the centre on the ring. This torque is given by
$\tau = FR$
From (5)
$\tau = 4q{R^2}t$ …………………………….(6)
But there is frictional force also present between the horizontal surface and the ring which will produce a counter torque, given by
$\tau ' = fR$ …………………………….(7)
From (6) the electric torque increases with time. The frictional torque will keep the net torque zero until the external torque reaches the maximum value of the frictional torque. We know that the maximum value of the frictional force is given by
$f = \mu N$
As the ring is placed on a horizontal surface, so $N = mg$ . Therefore
$f = \mu mg$
Substituting this in (7) we get
$\tau ' = \mu mgR$ …………………………….(8)
When the ring just starts rotating, the electric torque will be equal to the frictional torque, that is,
$\tau = \tau '$
From (6) and (8) we have
$4q{R^2}t = \mu mgR$
$\Rightarrow \mu = \dfrac{{4q{R^2}t}}{{mgR}}$
On simplifying we get
$\mu = \dfrac{{4qRt}}{{mg}}$
According to the question, the time $t = 2s$ . Substituting this above, we finally get
$\mu = \dfrac{{8qR}}{{mg}}$
Hence, the correct answer is option C.

Note
Similar to the case of translational motion, the concept of frictional torque is applicable. The frictional torque is equal to the external applied torque until the external torque equals the maximum value of the frictional torque.