Question

A non conducting disc of radius $R$, charge $q$ is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity $\omega$, charge $q$ is uniformly distributed over its surface. The magnetic moment of the disc is:
A. $\dfrac{1}{4}q\omega {R^2}$
B. $\dfrac{1}{2}q\omega R$
C. $q\omega R$
D. $\dfrac{1}{2}q\omega {R^2}$

Answer 1

To find the magnetic moment of the disc, first recall the formula for magnetic moment of a current loop. Take a small annular region of the disc and find the magnetic moment of this region and then integrate the value taking the limit of radius from zero to $R$, to find the value of magnetic moment of the whole disc.

Complete step by step answer:
Given, radius of a non conducting disc, $R$. Charge on the disc, $q$. Angular velocity of the disc, $\omega$. The magnetic moment of a current loop is given by the formula,
$\mu = IA$
where $I$ is the current through the loop and $A$ is the area of the loop.
Surface charge density is defined as charge per unit area. Here, area of the disc is $\pi {R^2}$ and charge is $q$ so, surface charge density will be,
$\sigma = \dfrac{q}{{\pi {R^2}}}$ (i)
Now, we take a small cross section such that its length is $dr$ with its inner radius is $r$ and outer radius is $r + dr$ and $dr < < r$.

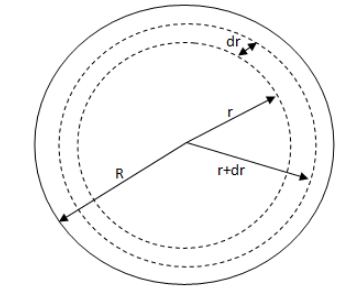
Here, surface charge density for this region will be,
$\sigma = \dfrac{{dq}}{{d\left( {\pi {r^2}} \right)}}$
$\Rightarrow \sigma = \dfrac{{dq}}{{2\pi rdr}}$
$\Rightarrow dq = 2\pi rdr\sigma$
Putting the value of $\sigma$ in the above equation we get,
$dq = 2\pi rdr\left( {\dfrac{q}{{\pi {R^2}}}} \right)$
$\Rightarrow dq = \dfrac{{2q}}{{{R^2}}}rdr$
The charge $dq$ completes one revolution in the time interval, $T = \dfrac{{2\pi }}{\omega }$
We know current is charge per unit time. So here current through this small region will be,
$dI = \dfrac{{dq}}{T}$
Putting the values of $dq$ and $T$ we get,
$dI = \dfrac{{\left( {\dfrac{{2q}}{{{R^2}}}rdr} \right)}}{{\left( {\dfrac{{2\pi }}{\omega }} \right)}}$
$\Rightarrow dI = \dfrac{{\left( {\dfrac{q}{{{R^2}}}rdr} \right)}}{{\left( {\dfrac{\pi }{\omega }} \right)}}$ (ii)

Area enclosed by this current is $A = \pi {r^2}$
So, magnetic moment due to this loop will be, (using equation (i))
$d\mu = dI \times A$
Putting the value of $dI$ and $A$ we get,
$d\mu = \dfrac{{\left( {\dfrac{q}{{{R^2}}}rdr} \right)}}{{\left( {\dfrac{\pi }{\omega }} \right)}} \times \pi {r^2}$
$\Rightarrow d\mu = \dfrac{{\omega q}}{{{R^2}}}rdr \times {r^2}$
$\Rightarrow d\mu = \dfrac{{\omega q}}{{{R^2}}}{r^3}dr$
Now, we get the magnetic moment of the disc by integrating on both sides of the above equation from $0$ to $R$ on right side and $0$ to $\mu$ on left side,
$\int\limits_0^\mu {d\mu } = \int\limits_0^R {\dfrac{{\omega q}}{{{R^2}}}{r^3}dr}$
$\Rightarrow \mu = \dfrac{{\omega q}}{{{R^2}}}\left[ {\dfrac{{{r^4}}}{4}} \right]_0^R$
$\Rightarrow \mu = \dfrac{{\omega q}}{{{R^2}}}\left[ {\dfrac{{{R^4}}}{4}} \right]$
$\therefore \mu = \dfrac{1}{4}q\omega {R^2}$
Therefore, the magnetic moment of the disc is $\dfrac{1}{4}q\omega {R^2}$.

Hence, the correct answer is option A.

Note: The magnetic moment can be defined as the magnetic strength and orientation of an object that produces a magnetic field. It is a vector quantity and direction of magnetic moment can be found using right hand rule, which is perpendicular to the current loop.