Question
Question: A nine similar resistors of resistance R are connected as shown in the figure. Find the equivalent r...
A nine similar resistors of resistance R are connected as shown in the figure. Find the equivalent resistance between points A and B.
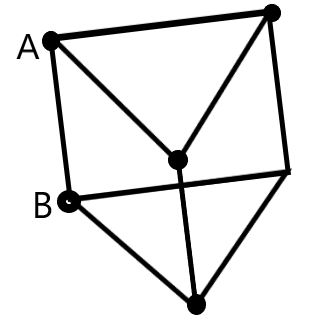
Solution
We are given a combination of resistances. We have to resolve them as in series or as in parallel to find the equivalent resistance of the circuit across the points A and B. We can resolve them easily by identifying the circuit closely.
Complete answer:
We need to resolve the resistors to understand whether they are in series or parallel to each other. Let us get a clearer idea of the network as –
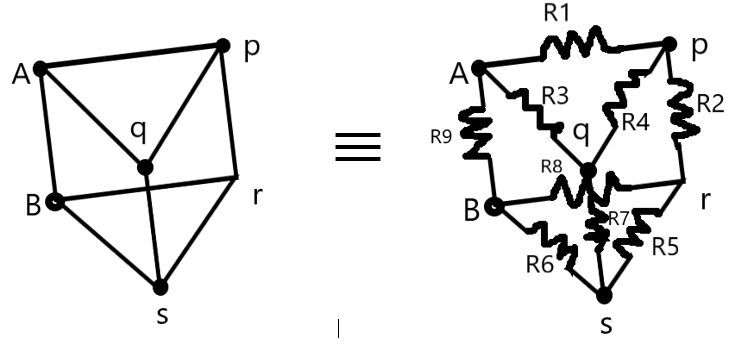
We can elaborate the connections as shown in the above diagram.
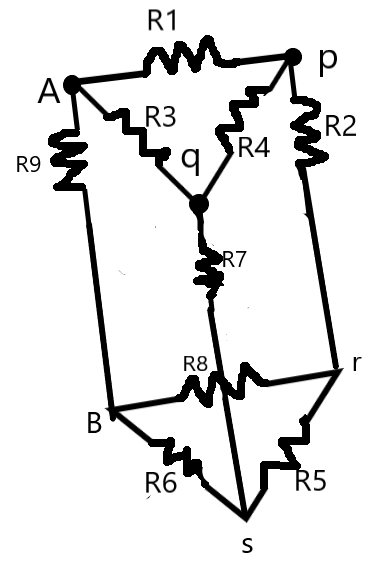
A closer approach to circuit will help us find two pairs of equipotential points in the circuit. From the Wheatstone’s bridge condition, we know that, a resistor in between two equipotential points due not play a role in the circuit, i.e., there will be no potential drop or current flow across these resistors.
The points p and q on the left arm of the circuit are at equal potentials as a result, the current through R4 is zero and thus, we can neglect the resistance R4.
Similarly, the points r and s are also at equal potentials, i.e., we can neglect the resistor R5. We get the resultant circuit as –
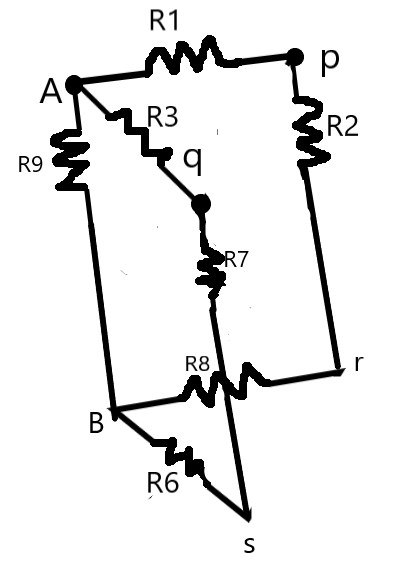 .
.
Now, we can find that the resistances (R1, R2, R8), (R3, R7, R6) are pairs of series resistors parallel to each other and to R9.
We can compute the equivalent resistance as –
