Question

A neutron travelling with a velocity v and K.E., It collides perfectly elastically head on with the nucleus of an atom of mass number A at rest. The fraction of total energy retained by the neutron is
$\begin{aligned} & A){{\left( \dfrac{A-1}{A+1} \right)}^{2}} \\\ & B){{\left( \dfrac{A+1}{A-1} \right)}^{2}} \\\ & C){{\left( \dfrac{A-1}{A} \right)}^{2}} \\\ & D){{\left( \dfrac{A+1}{A} \right)}^{2}} \\\ \end{aligned}$

Answer 1

For solving this question, we must have the basic idea about a neutron and its nature. Also, we will need to draw a diagram to understand the movement of the two bodies before and after the collision. Then by using the law of conservation of momentum, we can find the final velocity of a neutron. We must know that the coefficient of restitution for an elastic collision is 1.
Formula Used:
$\begin{aligned} & {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\\ & K.E=\dfrac{1}{2}m{{v}^{2}} \\\ & e=\dfrac{\text{velocity of separation after collision}}{\text{velocity of approach before collision}} \\\ \end{aligned}$

Complete answer:
It is given that the neutron is colliding elastically head on with the nucleus of the atom. We will draw a diagram to understand the situation better.

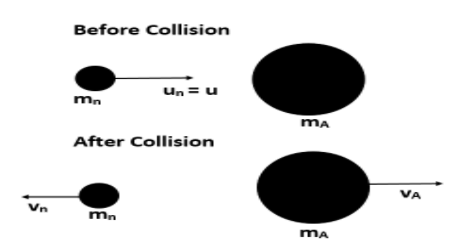
Now, let us consider the mass of the neutron as ${{m}_{n}}$ and the mass of the nucleus as ${{m}_{A}}$. we know that nucleus consist of both neutrons and protons and they have the same mass.
i.e. ${{m}_{n}}={{m}_{p}}=m$
Also, the mass number of an atom is given by the sum of the number of protons and neutrons in it.
Let us take the number of neutrons as x and number of protons as y. Then, mass of the nucleus will be,
$\begin{aligned} & {{m}_{A}}=x{{m}_{n}}+y{{m}_{p}} \\\ & {{m}_{A}}=\left( x+y \right){{m}_{n}} \\\ & {{m}_{A}}=\left( x+y \right)m=Am \\\ \end{aligned}$
Here, A is the mass number.
Now, by applying law of conservation of momentum to these two bodies,

& {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\\ & \Rightarrow {{m}_{n}}u+A{{m}_{n}}\times 0={{m}_{n}}\left( -{{v}_{1}} \right)+A{{m}_{n}}{{v}_{2}} \\\ & \Rightarrow {{m}_{n}}u=-{{m}_{n}}{{v}_{1}}+A{{m}_{n}}{{v}_{2}} \\\ & \Rightarrow u=A{{v}_{2}}-{{v}_{1}}\text{ -- (1)} \\\ \end{aligned}$$ Now, we know that the coefficient of restitution for an elastic collision is 1. That is, $e=\dfrac{\text{velocity of separation after collision}}{\text{velocity of approach before collision}}=1$ Here, velocity of separation after collision is the relative velocity between neutron and nucleus after collision. That is, $${{v}_{1}}+{{v}_{2}}$$ Also, the velocity of approach before collision is u. Then, $\begin{aligned} & e=\dfrac{{{v}_{1}}+{{v}_{2}}}{u}=1 \\\ & \Rightarrow u={{v}_{1}}+{{v}_{2}} \\\ & \Rightarrow {{v}_{2}}=u-{{v}_{1}}\text{ -- (2)} \\\ \end{aligned}$ Now, substituting (2) in (1), we will get, $$\begin{aligned} & \Rightarrow u=A\left( u-{{v}_{1}} \right)-{{v}_{1}} \\\ & \Rightarrow u=Au-A{{v}_{1}}-{{v}_{1}} \\\ & \Rightarrow {{v}_{1}}\left( A+1 \right)=u\left( A-1 \right) \\\ & \Rightarrow \dfrac{{{v}_{1}}}{u}=\dfrac{\left( A-1 \right)}{\left( A+1 \right)} \\\ \end{aligned}$$ So, the relation between initial and final velocity of the neutron is found to be $$\dfrac{{{v}_{1}}}{u}=\dfrac{\left( A-1 \right)}{\left( A+1 \right)}$$ . Now, we will take the ratio of initial and final kinetic energy and find the expression for a fraction of total energy. For that, we know, $K.E=\dfrac{1}{2}m{{v}^{2}}$ $\begin{aligned} & \dfrac{K.{{E}_{final}}}{K.{{E}_{initial}}}=\dfrac{\dfrac{1}{2}m{{\left( {{v}_{1}} \right)}^{2}}}{\dfrac{1}{2}m{{\left( u \right)}^{2}}}=\dfrac{{{\left( {{v}_{1}} \right)}^{2}}}{{{\left( u \right)}^{2}}} \\\ & \Rightarrow {{\left( \dfrac{{{v}_{1}}}{u} \right)}^{2}}={{\left( \dfrac{A-1}{A+1} \right)}^{2}} \\\ \end{aligned}$ Therefore, the fraction of the total energy retained by the neutron is ${{\left( \dfrac{A-1}{A+1} \right)}^{2}}$ **So, option A is correct.** **Note:** We must know that in case of elastic collision, we need to consider the momentum before and after the collision takes place. Also, we need to keep in mind the law of conservation of momentum to solve these types of questions.