Question

A neutron moving with velocity u, collides elastically with an atom of mass number A. If the collision is head on and the kinetic energy of neutron is E, then the final kinetic energy of neutron after collision is-

A.)${\left( {\dfrac{{1 - A}}{{1 + A}}} \right)^2}E$
B.)${\left( {\dfrac{{1 + A}}{{1 - A}}} \right)^2}E$
C.)${\left( {\dfrac{{A - 1}}{{A + 1}}} \right)^2}E$
D.)${\left( {\dfrac{{A + 1}}{{A - 1}}} \right)^2}E$

Answer 1

Hint: First, we will let the number of protons and the number of neutrons inside the nucleus be x and y. then we will find out the mass of the nucleus and apply the law of conservation of momentum.

Complete step by step answer:
Formula used: $K = \dfrac{1}{2}m{v^2}$.

Let the mass of the neutron $\left( {{m_n}} \right)$ be-

$\Rightarrow {m_n} = m$

If there is a nucleus whose mass number is A, it must have some number of neutrons and protons. Let the number of neutrons be y and the number of protons be x. Thus, its mass number A will be-

$\Rightarrow$A = number of protons + number of neutrons

$\Rightarrow A = x + y$

As we know that the mass of a neutron is equal to the mass of a proton. We let the mass of the neutron be m. Hence, mass of the proton will be-

$\Rightarrow {m_p} = m = {m_n}$

Mass of a neutron is m, so the mass of y number of neutrons will be ym.
Mass of a proton is m, so the mass of x number of protons will be xm.

Mass of the nucleus will be-

$\Rightarrow {m_A} = xm + ym \\\ \\\ \Rightarrow {m_A} = \left( {x + y} \right)m \\\$

As we know that A was equal to (x+y). so-

$\Rightarrow {m_A} = \left( {x + y} \right)m \\\ \\\ \Rightarrow {m_A} = Am \\\$

We can apply the law of conservation of momentum for collision because the force applied by the neutron on the nucleus will be equal to the force applied by the nucleus on the neutron. Hence, the net force will be zero.

Thus, we can say that initial momentum is equal to the final momentum-

$\Rightarrow {p_i} = {p_f}$

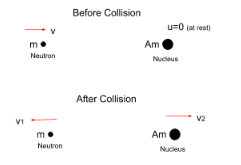
Initially, the nucleus had no momentum as it was at rest. The initial momentum before collision of the neutron will be mv. Where, m denotes the mass and v denotes the velocity of the neutron.

Finally, after collision, the momentum of the neutron will be $- m{v_1}$ (as the velocity is in negative direction). And the momentum of the nucleus after collision will be $Am{v_2}$.
Putting all these values, we get-

$\Rightarrow {p_i} = {p_f} \\\ \\\ \Rightarrow mv = - m{v_1} + Am{v_2} \\\ \\\ \Rightarrow v = A{v_2} - {v_1} \\\$

Let the above equation be equation 1.

$\Rightarrow v = A{v_2} - {v_1}$ (equation 1)

It was given that the neutron collides elastically which means that e is equal to 1. The formula for e is velocity of separation after collision divided by velocity of approach before collision. As we can see from the figure that after the collision, both the neutron and the nucleus are increasing the separation by moving into opposite directions. So, the velocity of net separation will be-

$\Rightarrow {v_1} + {v_2}$

As we can see from the figure that before the collision, neutron is approaching the nucleus with velocity v. So, the velocity of approach before collision will be-

$\Rightarrow v$

Thus, the value of e will be-

$\Rightarrow 1 = \dfrac{{{v_1} + {v_2}}}{v} \\\ \\\ \Rightarrow {v_1} + {v_2} = v \\\$

Multiplying the above equation by A on the both sides-

$\Rightarrow Av = A{v_1} + A{v_2}$

Let the above equation be equation 2.

$\Rightarrow Av = A{v_1} + A{v_2}$ (equation 2)

Subtracting equation 1 from equation 2, we get-

$\Rightarrow Av - v = A{v_1} + A{v_2} - A{v_2} + {v_1} \\\ \\\ \Rightarrow Av - v = A{v_1} + {v_1} \\\ \\\ \Rightarrow v\left( {A - 1} \right) = {v_1}\left( {A + 1} \right) \\\ \\\ \Rightarrow {v_1} = v\dfrac{{\left( {A - 1} \right)}}{{\left( {A + 1} \right)}} \\\$

Now, we considered ${v_1}$ as the velocity of a neutron.

Hence, the kinetic energy after collision will be-

$\Rightarrow K = \dfrac{1}{2}m{v_1}^2 \\\ \\\ \Rightarrow K = \dfrac{1}{2}m{v^2}{\left( {\dfrac{{A - 1}}{{A + 1}}} \right)^2} \\\$

Since we knew that initially, kinetic energy of neutron was E and the speed was v. Thus, the initial kinetic energy will be-

$\Rightarrow E = \dfrac{1}{2}m{v^2}$
Thus,

$\Rightarrow K = \dfrac{1}{2}m{v^2}{\left( {\dfrac{{A - 1}}{{A + 1}}} \right)^2} \\\ \\\ \Rightarrow K = E{\left( {\dfrac{{A - 1}}{{A + 1}}} \right)^2} \\\$

Hence, it is clear that option C is the correct option.

Note: Kinetic energy, the energy source which an entity or a particle has through its movement. When work that converts energy through an object is carried out by using a net force, the object accelerates and absorbs kinetic energy. Kinetic energy is a function of a moving body or component which is not only dictated by acceleration but also by mass.