Question

A neutron moving with speed $\nu$ makes a head on collision with a hydrogen atom in ground state kept at rest. The minimum kinetic energy of the neutron for which inelastic collision takes place is
$\begin{aligned} & A)10.2eV \\\ & B)20.4eV \\\ & C)12.1eV \\\ & D)16.8eV \\\ \end{aligned}$

Answer 1

Students can use the idea that in case of inelastic collision, the momentum before and after the collision will remain the same, that is, in inelastic collision, momentum remains conserved. But, a particular amount of energy is released after the collision which must be added to the energy term which is considered after the collision.

Complete step by step solution:

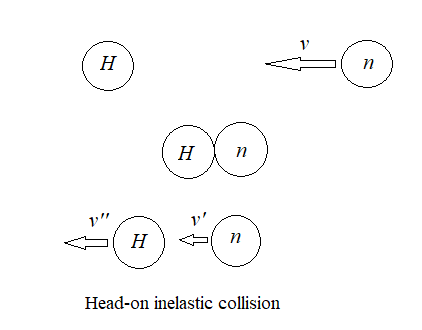
In the above figure, a neutron n is moving with a velocity $\nu$as given in the question. It undergoes a head-on collision with a hydrogen atom H at rest and after collision, the velocity of the neutron changes to $\nu '$ and the velocity of the hydrogen atom changes to $\nu ''$. Let us consider that the energy released after the collision is $\Delta E$. As the masses of both the neutron and hydrogen are different by only a negligible amount, so we can consider them to be the same, that is we consider their masses to be $m$.
Therefore,
By law of conservation of momentum,
$mv=mv'+mv''$… $equation(1)$
Also,
$\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}mv{{'}^{2}}+\dfrac{1}{2}mv{{''}^{2}}+\Delta E$…$equation(2)$
Now from $equation(1)$ and $equation(2)$, we can write,
$\begin{aligned} & \text{v=v }\\!\\!'\\!\\!\text{ +v''} \\\ & \text{and} \\\ & {{\text{v}}^{\text{2}}}\text{=v}{{\text{ }\\!\\!'\\!\\!\text{ }}^{\text{2}}}\text{+v}{{\text{''}}^{\text{2}}}\text{+}\dfrac{\text{2 }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ \end{aligned}$
$\begin{aligned} & \text{Since,(v}{{\text{ }\\!\\!'\\!\\!\text{ }}^{\text{2}}}\text{+v}{{\text{''}}^{\text{2}}}\text{)=(v }\\!\\!'\\!\\!\text{ +v''}{{\text{)}}^{\text{2}}}\text{-2 }\\!\\!\times\\!\\!\text{ v }\\!\\!'\\!\\!\text{ }\\!\\!\times\\!\\!\text{ v''} \\\ & \text{therefore,}{{\text{v}}^{\text{2}}}\text{=(v }\\!\\!'\\!\\!\text{ +v''}{{\text{)}}^{\text{2}}}\text{-2 }\\!\\!\times\\!\\!\text{ v }\\!\\!'\\!\\!\text{ }\\!\\!\times\\!\\!\text{ v''+}\dfrac{\text{2 }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ & \text{Again,as,v=v }\\!\\!'\\!\\!\text{ +v''} \\\ & \text{therefore,}{{\text{v}}^{\text{2}}}\text{=}{{\text{v}}^{\text{2}}}\text{-2 }\\!\\!\times\\!\\!\text{ v }\\!\\!'\\!\\!\text{ }\\!\\!\times\\!\\!\text{ v''+}\dfrac{\text{2 }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ & \Rightarrow \dfrac{\text{ }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}}\text{=v }\\!\\!'\\!\\!\text{ }\\!\\!\times\\!\\!\text{ v''} \\\ & \Rightarrow \text{v }\\!\\!'\\!\\!\text{ }\\!\\!\times\\!\\!\text{ v''=}\dfrac{\text{ }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ \end{aligned}$
$\begin{aligned} & \text{Again,(v }\\!\\!'\\!\\!\text{ -v''}{{\text{)}}^{\text{2}}}\text{=(v }\\!\\!'\\!\\!\text{ +v''}{{\text{)}}^{\text{2}}}\text{-4 }\\!\\!\times\\!\\!\text{ v }\\!\\!'\\!\\!\text{ }\\!\\!\times\\!\\!\text{ v''} \\\ & \Rightarrow {{\text{(v }\\!\\!'\\!\\!\text{ -v'')}}^{\text{2}}}\text{=}{{\text{v}}^{\text{2}}}\text{-4 }\\!\\!\times\\!\\!\text{ }\dfrac{\text{ }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ & \text{As,(v }\\!\\!'\\!\\!\text{ -v''}{{\text{)}}^{\text{2}}}\ge \text{0} \\\ & \text{therefore,}{{\text{v}}^{\text{2}}}\ge \text{4 }\\!\\!\times\\!\\!\text{ }\dfrac{\text{ }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ & \Rightarrow {{\text{v}}^{\text{2}}}\ge \text{4 }\\!\\!\times\\!\\!\text{ }\dfrac{\text{ }\\!\\!\Delta\\!\\!\text{ E}}{\text{m}} \\\ \end{aligned}$
Multiplying both sides of the equation by $\dfrac{1}{2}m$, we get,
$\dfrac{1}{2}m{{v}^{2}}=2\times \Delta E$
The minimum energy absorbed by a hydrogen atom in moving from ground state to first excited state is $10.2eV$.
Therefore ,
$\begin{aligned} & \dfrac{1}{2}m{{v}^{2}}=2\times \Delta E \\\ & \Rightarrow \dfrac{1}{2}m{{v}^{2}}=2\times 10.2eV \\\ & \Rightarrow \dfrac{1}{2}m{{v}^{2}}=20.4eV \\\ & \\\ \end{aligned}$
The minimum kinetic energy of the neutron is $20.4eV$.
The required answer to the question is option $B)20.4eV$.

Note: If the collision is elastic, both the energy and momentum will be conserved. In that case, we do not need to add an extra term in the equation of energy. In this question, the collision is inelastic, for which we have added an extra term for energy.