Question

A network of four capacitors of 6μF each is connected to a 240V supply. Determine the charge on each capacitor.

Answer 1

A capacitor is a device used to store an electric charge, consisting of one or more pairs of conductors separated by an insulator.
Capacitors can be added to an electrical circuit either in parallel connection or series connection in both cases the equivalent resistance is calculated in the OPPOSITE way as it is calculated for resistance in series or resistance in parallel.

Complete step by step solution:
Here the capacitors are arranged in a square formation
Or in other words, we can see that capacitors ${C_1},{C_2},{C_3}$ are in series connection and their equivalent conductance will be in parallel connection with capacitor c4
Here this setup is provided a 240 v across it
Now, if capacitors are connected in series connection their equivalent conductance will be given by
$\dfrac{1}{{C`}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
Here in this case capacitors ${C_1},{C_2},{C_3}$ are connected in series connection so their equivalent resistance will be

$$\dfrac{1}{{C`}} = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} \\\ \Rightarrow \dfrac{1}{{C`}} = \dfrac{3}{6} \\\ \Rightarrow \dfrac{1}{{C`}} = \dfrac{1}{2} \\\ \Rightarrow C` = 2\mu F \\\$$

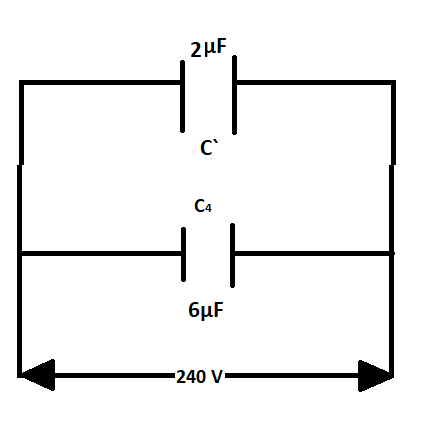
Now our circuit diagram looks like
Now as we can see that the equivalent capacitance $C`$and capacitor ${C_4}$are in parallel connection
If two capacitors are in parallel connection their equivalent capacitance is given by
$C`` = {C_1} + {C_2}$
In this case, the equivalent capacitance will be
$C`` = C` + {C_4} \\\ \therefore C`` = 2 + 6 \\\ \Rightarrow C`` = 8\mu F \\\$
So, the total equivalent capacitance of the circuit is $8\mu F$
Now, the amount of charge flowing in the circuit is given by
$q = CV$
Where
$q$ is the charge flowing in the circuit
$C$ is the equivalent capacitance
$V$ is the voltage applied
So the amount of charge flowing across capacitors ${C_1},{C_2},{C_3}$ which are connected in series will be
Given values,
$C = 2\mu F$
Since here capacitance is given in micro Farad we need to convert it into Farad
$\because 1\mu F = {10^{ - 6}}F \\\ \therefore 1\mu F = 2 \times {10^{ - 6}}F \\\$
So,
$\because q = CV$
$\therefore q = 2 \times {10^{ - 6}} \times 240$
$\Rightarrow q = 4.8 \times {10^{ - 4}}C$
This charge will be flowing across each of the capacitors ${C_1},{C_2},{C_3}$which are in series
Now across capacitor ${C_4}$
Again
$\because q = CV$
$\therefore q = 6 \times {10^{ - 6}} \times 240$
$\Rightarrow q = 1.44 \times {10^{ - 3}}C$
So $1.44 \times {10^{ - 3}}C$ will be the charge flowing across ${C_4}$

The charge flowing across capacitors ${C_1},{C_2},{C_3}$will be $4.8 \times {10^{ - 4}}C$ and the charge flowing across the capacitor ${C_4}$ will be $1.44 \times {10^{ - 3}}C$.

Note: The charge flowing will be divided into two streams one stream will be flowing through capacitors ${C_1},{C_2},{C_3}$ and the other will be flowing across capacitors ${C_4}$ this is the reason why there is a difference between the charges flowing through these capacitors.
Capacitors act as the charge storing devices, in alternating current the store the charge and maintain a positive cycle for AC. Thus saves the change of polarity and helps in the functioning of the electric motors.