Question

A nearly massless rod is pivoted at one end so that it can swing freely like a pendulum. Two masses $m$ and $2m$ are attached to it at distances $b$ and $3b$respectively from the pivot. The rod is held horizontal and then released. The angular acceleration of the rod at the instant it is released is
$(a)bg$
$(b)\dfrac{b}{g}\;$
$(c)bg + 5\;$
$(d)\dfrac{{5g}}{{11b}}$

Answer 1

From the question, we can take that the masses separated by the given distances experience a torque when in rotation. This rotational torque is related to its angular acceleration by taking into consideration its moment of inertia and the distance between the two. Finally, by equating the two relations we will be able to obtain the value of the torque.

Complete step-by-step solution:
A nearly massless rod is pivoted at one end and is separated by distances $b$ and $3b$ which is as shown below such that it can swing freely like a pendulum attached to it of masses $m$ and $2m$

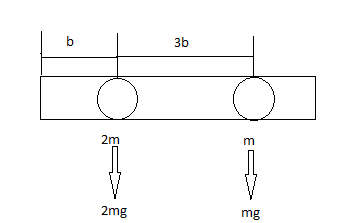
When a torque is applied to an object it starts to rotate with an acceleration that is inversely proportional to its moment of inertia $I$. This relation is called Newton’s Second Law for rotation.
Initially, we find the torque that is given by
Torque$\tau = \,m \times r$ we get for different masses at distances
$\tau = \,(2mg \times b + \,mg \times 3b)$
$\tau = 5mgb$…..this is equation 1
Also, the moment of inertia for the rods could be derived and is given by $I = \,m{r^2}$
For masses $m$ and $2m$ at distances, $b$ and $3b$ we get the moment of inertia is
${I_1} = 2m{b^2}$
And ${I_2} = 9m{b^2}$
Therefore, $I = {I_1} + {I_2} = 11m{b^2}$……this is equation 2
If it's a frictionless pendulum that keeps on swinging forever (unless there's air friction), here we relate the angular acceleration to the moment of inertia and torque
Torque $\tau = \,I \times \alpha$
We get from the equation 1 and 2
$\tau = \,5m{b^2} \times \alpha$
$5mgb = 11m{b^2} \times \alpha$
From this equation, we conclude $\alpha = \dfrac{{5g}}{{11b}}$(option D)

Note: It is sure to obtain the required torque for the two masses that are being placed at different distances when it is taken as a pendulum that is freely rotating. This rotational inertia depends upon the mass of an object and how it is distributed to the axis of rotation. This also helps to determine how much force it would take to rotate a body.