Question
Question: A naughty girl sits stationary at the back end of a long trolley moving uniformly with speed\(v\)on ...
A naughty girl sits stationary at the back end of a long trolley moving uniformly with speedvon a smooth horizontal floor. If she gets up and runs forward, then the speed of the center of mass (trolley and girl) system:
A) Increases
B) Decreases
C) Remains the same
D) Depends on the speed of girl
Solution
When the system is isolated i.e. the physical system is so far removed from the other system (that it does not interact with them) and no force is acting on it, the speed of center of mass does not change.
Complete step by step answer:
t is given that the long trolley is moving with the constant speed v.
So, when the girl is sitting on the floor of the trolley, the entire system is moving with the constant speed and hence, the speed of the center of mass is constant.
Now, if the girl stands up and starts to run on the trolley, she would still be on the trolley. That means, by her running, the speed of the trolley is not changing.
Thus, even though the girl is not stationary any more. She is still stationary compared to the entire system of trolley and girl as the speed of the system is not changing because of her movement. Thus, no additional force is applied to the total system.
Hence, the speed of center of mass of the system of trolley and girl will not change.
Therefore, from the above explanation we can conclude that option C is the correct one.
Additional information:
Center of mass:
Center of mass is a position defined relative to an object or system of objects. It is the average position of all the parts of the system, weighted according to their masses. Sometimes the center of mass does not fall anywhere on the object.
Formula of center of mass:
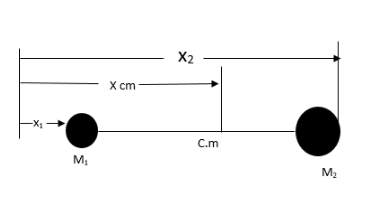
xcm=m1+m2m1x1+m2x2
Note: The center of mass does not need to be located within the object itself. For simple rigid objects with uniform density the center of the mass is located at the centroid. Example, the center of mass of disc shape would be at its center.
