Question

A narrow capillary tube when dipped in a beaker containing water, the rise is $20cm$. If the area of cross-section of the bore is reduced to $\dfrac{1}{4}th$ value, water will rise to a height of.
A. $10\,cm$
B. $20\,cm$
C. $40\,cm$
D. $80\,cm$

Answer 1

We know capillarity is the phenomenon of rise and fall of liquid in a narrow cross-section with respect to the adjacent layer of liquid in a beaker. The narrow cross-section can be capillary tube or any other narrow tube, must be opened at one end. In order to calculate change in height due to change in area of bore( which is nothing but the area of the opening of narrow tube), it can be done by using formulas of rise of water due to capillary action and taking ratio of initial and final height will get our answer.

Formula used:
The formula to find the rise in capillary tube is
$H = \dfrac{{4\sigma \cos \theta }}{{\rho g{d_{}}}}$
where $H$ is the rise in height due to capillary effect, $\sigma$ is the surface tension in liquid, $g$ is the gravitational acceleration acting on water, $\rho$ is density of liquid , $d$ is diameter of capillary tube and $\theta$ is angle of contact.

Complete step by step answer:
We know that when a capillary tube opens at its end dipped in water, then there will be rise and fall of liquid in the tube and this occurs due to cohesion and adhesion forces acting between water molecule and tube surface, this causes rise in surface tension effect also.Capillary rise will only take place when adhesion force, which is attraction force between water molecule and tube surface is more as compared to cohesion force.

As we are asked to find the change in height due to change in the area of cross-section of bore of capillary tube where bore is nothing but the area of opening of narrow tube or we can say diameter of tube, so in order to find change consider the figure given below.Here, initially the capillary tube is dipped having area of cross-section ${A_1}$ and diameter ${d_1}$, and rise of water in tube is ${H_1}$ .

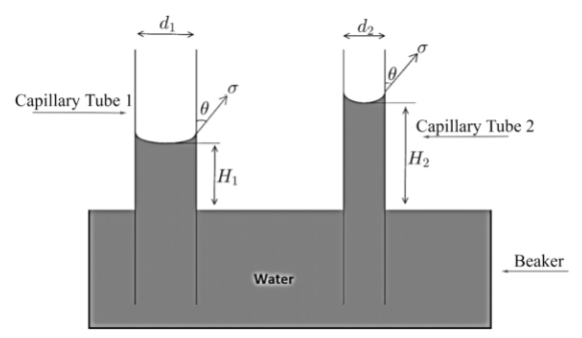
While in second case, the capillary tube which is dipped having area of cross-section
${A_2} = \dfrac{1}{4}{A_1}$ ………. $\left( 1 \right)$ ( As given in question area of cross-section of second tube is reduced by $\dfrac{1}{4}{A_1}$), and diameter ${d_2}$ and rise of water in tube is ${H_2}$. Here one important point to note is that as water in both cases is same so density $\left( \rho \right)$ and surface tension $\left( \sigma \right)$ as well angle of contact $\left( \theta \right)$ will remain same.

As given in the question ${H_1} = 20cm$. Now by using formula of capillary rise for tube $1$,
${H_1} = \dfrac{{4\sigma \cos \theta }}{{\rho g{d_1}}}$………………… $\left( 2 \right)$.
Now we know cross-section area of tube $1 = \pi {\left( {\dfrac{{{d_1}}}{2}} \right)^2}$ and similarly cross-section area of tube$2 = \pi {\left( {\dfrac{{{d_2}}}{2}} \right)^2}$.
Now substituting this value in equation $\left( 1 \right)$,
$\pi {\left( {\dfrac{{{d_2}}}{2}} \right)^2} = \dfrac{1}{4}\pi {\left( {\dfrac{{{d_1}}}{2}} \right)^2}$ , from here we get ${d_2} = \dfrac{1}{2}{d_1}$ …………… $\left( 3 \right)$.
Now similarly for capillary rise in tube 2 ,
${H_2} = \dfrac{{4\sigma \cos \theta }}{{\rho g{d_2}}}$ ………………………… $\left( 4 \right)$.

Now taking the ratio of equation $\left( 4 \right)$ and $\left( 2 \right)$ we will get,
$\dfrac{{{H_2}}}{{{H_1}}} = \dfrac{{4\sigma \cos \theta }}{{\rho g{d_2}}} \times \dfrac{{\rho g{d_1}}}{{4\sigma \cos \theta }}$,
and now substituting the value of ${d_1}$ in ${d_2}$ as in equation $\left( 3 \right)$ will get,
$\dfrac{{{H}_{2}}}{{{H}_{1}}}=\dfrac{4\sigma \cos \theta }{\rho g\dfrac{1}{2}{{d}_{1}}}\times \dfrac{\rho g{{d}_{1}}}{4\sigma \cos \theta }$
Now further simplifying this we will get our final equation,
$\dfrac{{{H}_{2}}}{{{H}_{1}}}=2$
${{H}_{2}}=2{{H}_{1}}$
Substituting the value of $H_1$ we get the final answer,
$\therefore {{H}_{2}}=2\times 20=40\,cm$
Hence by reducing the area of cross-section of bore the rise in height will be $40cm$.

Hence the option C is the correct answer.

Note: The capillary rise take place only when adhesion force is greater than cohesion force otherwise capillary fall takes mostly in the case when liquid is mercury, due to rise of liquid meniscus will form at the surface as shown in figure its because of the phenomenon of surface tension, and formula for the height of capillary fall is similar as capillary rise.