Question
Question: A multi-range current meter can be constructed by using a galvanometer circuit as shown in fig. We w...
A multi-range current meter can be constructed by using a galvanometer circuit as shown in fig. We want a current meter that can measure 10mA, 100mA and 1A using a galvanometer of resistance 10Ω and that produces maximum deflection for current of 1mA. Find S1,S2,S3that have to be used.
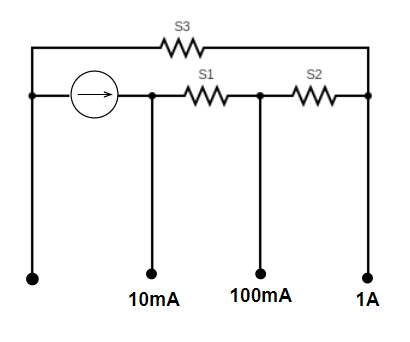
Solution
In order to construct a multi-range current meter, we would first need to understand the direction of flow of these currents through their respective shunt resistance. We will first calculate the net shunt resistance of the circuit using its formula and this net shunt will be equal to the sum of all shunt resistance in the series.
Complete answer:
Let us first assign some terms that we are going to use later in our solution.
Let us the net shunt resistance of the circuit be ‘S’, such that:
⇒S=S1+S2+S3 [Let this expression be equation number (1)]
Also, let the galvanometer current be IG. Then, it is given that:
⇒IG=1mA
Now, in the first case:
⇒I=10mA
Therefore, we can write:
⇒S=I−IGIG×G⇒S=10−11×10Ω⇒S=910Ω
Thus, putting this in equation (1), we get:
⇒S1+S2+S3=910Ω [Let this expression be equation number (2)]
Now, in the second case (G to S1), we have:
⇒I=100mA
⇒G′=G+S1
And, S=S2+S3
Therefore, we can write:
⇒(S2+S3)=I−IG(G+S1)×IG⇒(S2+S3)=99(10+S1)×1Ω
⇒(S2+S3)=99(10+S1)Ω [Let this expression be equation number (3)]
Now, in the third case (G to S2), we have:
⇒I=100mA
⇒G′′=G+S1+S1
And, S′′=S3
Therefore, we can write:
⇒(S3)=I−IG(G+S1+S2)×IG⇒(S3)=999(10+S1+S2)×1Ω
⇒S3=999(10+S1+S2)Ω [Let this expression be equation number (4)]
Now, putting equation (3) in equation (2), we get:
⇒S1+99G+S1=910∴S1=1Ω
Now, putting the value of S1in equation (3), we get:
⇒S2+S3=91Ω [Let this expression be equation number (5)]
And, putting the value of S1in equation (4), we get:
⇒S3−999S2=99911 [Let this expression be equation number (6)]
Solving equation number (5) and (6), we get:
⇒S2=0.1Ω⇒S3=0.011Ω
Hence, the value of S1,S2 and S3 comes out to be 1Ω,0.1Ω and 0.011Ω respectively.
Note:
In solving problems like these, we should understand the multiple connections correctly. Error in any one connection could render our complete solution wrong. Also, while performing lengthy calculations, one should be careful at each step of the process.
