Question

A moving block of mass m, collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of the coefficient of restitution (e) will be:
A. 0.8
B. 0.5
C. 0.4
D. 0.25

Answer 1

Use the law of conservation of linear momentum. Using this law, find the velocity of the heavier block just after the collision. Take the ratio of relative change in velocity of the heavier block and the relative change in velocity of lighter block. This will give the value of restitution.

Complete step-by-step solution:

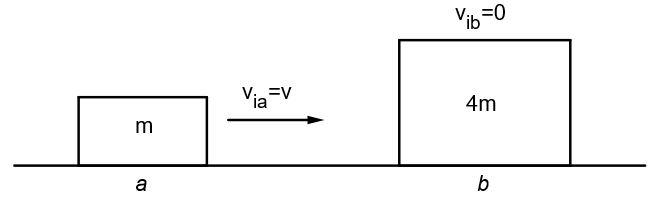
Applying law of conservation of linear momentum, we get
${ m }_{ a }{ v }_{ ia }+{ m }_{ b }{ v }_{ ib }={ m }_{ a }{ v }_{ fa }+{ m }_{ b }{ v }_{ fb }$ …(1)
Where, ${ m }_{ a }$ and ${ m }_{ b }$ are the masses which are given as m and 4m
${ v }_{ ia }$ and ${ v }_{ ib }$ are the initial velocities of blocks with mass m and 4m respectively
${ v }_{ fa }$ and ${ v }_{ fb }$ are the final velocities of blocks with mass m and 4m respectively
Given: ${ v }_{ ia }$=v
${ v }_{ ib }$=0
${ v }_{ fa }$=0
Simplifying equation.(1) we get,
${ m }_{ a }{ v }_{ ia }={ m }_{ a }{ v }_{ fb }$
Substituting the values in above equation we get,
${ m }{ v }={ 4m }{ v }_{ fb }$
$\Rightarrow { v }_{ fb }=\dfrac { v }{ 4 }$
$\Rightarrow { v }_{ fb }=0.25v$
Now, formula for coefficient of restitution is given by,
$e=\dfrac { \left( { v }_{ fa }-{ v }_{ fb } \right) }{ \left( { v }_{ ib }- { v }_{ ia } \right) }$
$\Rightarrow e=\dfrac { \left( 0-{ 0.25v } \right) }{ \left( 0-v \right) }$
$\Rightarrow e=\dfrac { -0.25v }{ -v }$
$\Rightarrow e=0.25$
Therefore, the value of coefficient of restitution is 0.25. Hence, the correct answer is option D i.e. 0.25.

Note: The coefficient of restitution tells us about the collision of masses. It states whether the collision was elastic or inelastic. If its value is 1 then the collision is an elastic collision, But, if its value is in the range from 0 to 1 then the collision is an inelastic collision.