Question

A motorcyclist riding motorcycle A, who is travelling at $36{\text{ km }}{{\text{h}}^{ - 1}}$applies the brakes and stops the motorcycle in$10{\text{ s}}$. Another motorcyclist of motorcycle B, who is travelling at${\text{18 km }}{{\text{h}}^{ - 1}}$, applies the brakes and stops the motorcycle in$20{\text{ s}}$. Plot speed-time graphs for the two motorcycles. Which of the two motorcycles travelled farther before it came to a stop?

Answer 1

The equations of motion in physics are defined as equations that describe the behavior of a physical system in terms of its motion as a function of time. There are three equations of motion which help us to derive the velocity, time, displacement and acceleration.

Complete step by step answer:
Find the initial velocities of both motorcycles and substitute them in the equation of motion to calculate acceleration. With the help of this acceleration and initial velocity, we can draw the graph. Consider the motorcycle A:
${u_A} = 36{\text{ km }}{{\text{h}}^{ - 1}} \\\ \Rightarrow {u_A}= 36 \times \dfrac{5}{{18}}{\text{ m se}}{{\text{c}}^{ - 1}} \\\ \Rightarrow {u_A}= 10{\text{ m se}}{{\text{c}}^{ - 1}}$
From the equations of motion, final velocity can be expressed as:
$v = u + at$
$\Rightarrow 0 = 10 + a \times 10$
$\Rightarrow a = - 1{\text{ m se}}{{\text{c}}^{ - 2}}$
From the equations of motion, final velocity can be expressed as:
Speed-time relation: $v = 10 - t$
Rearrange the terms so that the equation represents the equation of a straight line.
$v = - t + 10$

From this equation, we can draw the graph as follows:

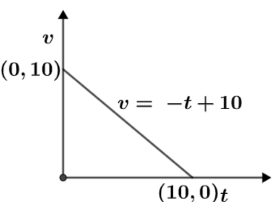
From the equations of motion, distance can be expressed as:
$S = ut + \dfrac{1}{2}a{t^2}$
$\Rightarrow S = 10 \times 10 + \dfrac{1}{2}( - 1){(10)^2} \\\ \Rightarrow S= 50{\text{ m}}$
Consider the motorcycle B:
${u_B} = 18{\text{ km }}{{\text{h}}^{ - 1}} \\\ \Rightarrow {u_B} = 18 \times \dfrac{5}{{18}}{\text{ m se}}{{\text{c}}^{ - 1}} \\\ \Rightarrow {u_B} = 5{\text{ m se}}{{\text{c}}^{ - 1}}$
From the equations of motion, final velocity can be expressed as:
$v = u + at$
$\Rightarrow v = 5 + a \times 20$
$\Rightarrow 0 = 5 + 20a$
$\Rightarrow a = - \dfrac{1}{4}$

From the equations of motion, final velocity can be expressed as:
Speed-time relation: $v = 5 - \dfrac{1}{4}t$
Rearrange the terms so that the equation represents the equation of a straight line.
$v = - \dfrac{t}{4} + 5$
From this equation, we can draw the graph as follows:

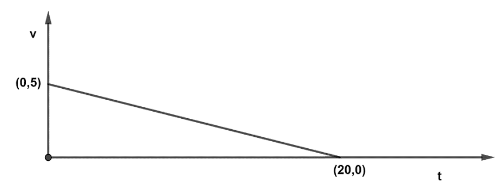
From the equations of motion, distance can be expressed as:
$S = ut + \dfrac{1}{2}a{t^2}$
$\Rightarrow S = 5 \times 20 + \dfrac{1}{2}\left( { - \dfrac{1}{4}} \right){(20)^2}$
$\therefore S = 100 - 50 = 50{\text{ m}}$
We can observe that both A and B covered the same distance.

Therefore, both motorcycles travelled the same distance before they came to a stop.

Note: The slope of the line on a velocity-time graph gives us useful information about the acceleration of the object. Acceleration of a body can be defined as the rate of change of velocity of that object with respect to time. A negative slope means the acceleration is negative. A downward sloping line indicates that the slope is negative.