Question

A motorcyclist moving with uniform retardation takes $10s$ and $20s$ to travel successive quarter kilometres. How much further will he travel before coming to rest?

Answer 1

Hint Such type of question can be solved by using Newton’s law of motion. Here motorcyclists move with uniform retardation which means there is a uniform negative acceleration. We will use Newton’s law of motion to find the velocity at which the motorcyclist is moving and by using we will find the distance covered by the motorcyclist before coming to rest.
Formula used:
Newton’s law of motion
$d = ut + \dfrac{1}{2}a{t^2}$
$\Rightarrow 2ad = {v^2} - {u^2}$

Complete Step by step answer

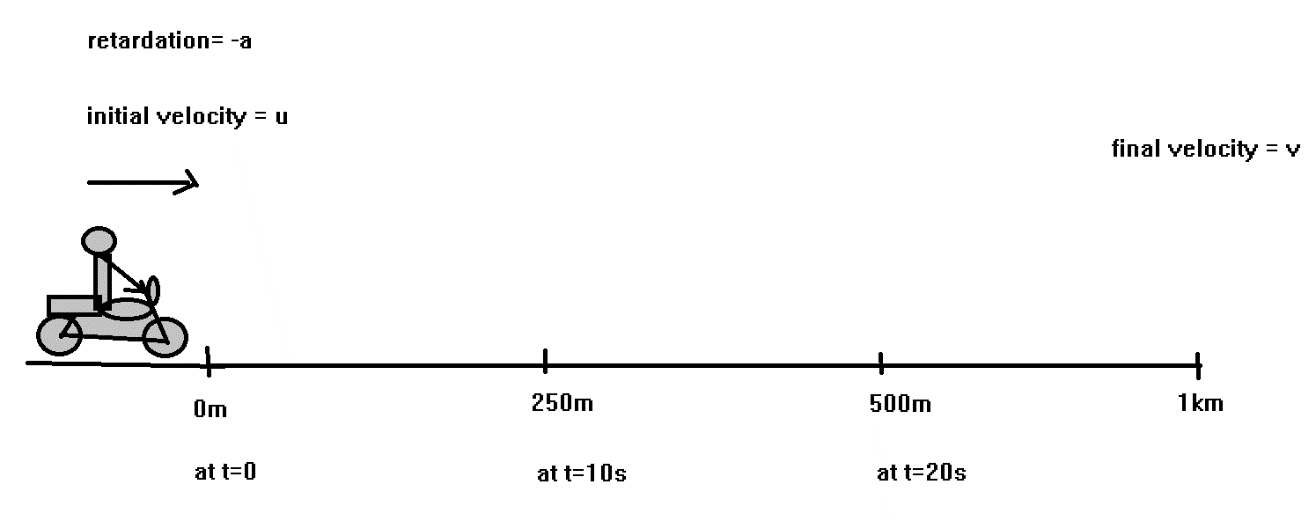
As we can see from the figure the motorcyclist moving with uniform retardation $- a\,m/{s^2}$ and initial velocity $u$. As he is moving successive quarter kilometers so time at $t = 10s$we will cover $250m$ and now he will take $t = 20s$to travel $500m$which means that from the starting point he will take total time $t = 30s$to cover $500m$the distance.
Now from Newton’s law of motion can be given as
$d = ut + \dfrac{1}{2}a{t^2}$
For the first quarter, he takes $t = 10s$to covers $d = 250m$
$\therefore 250 = 10u - \dfrac{1}{2}a \times {10^2}$ (Here $- a$ is retardation)
$\Rightarrow 25 = u - 5a$ -------------------- Equation $(1)$
Now for the second quarter, he takes a total $t = 30s$ to cover $d = 500m$ from the starting point. Hence
$500 = 30u - \dfrac{1}{2}a \times {30^2}$
On further solving the equation we get,
$50 = 3u - 45a$
$\Rightarrow \dfrac{{50}}{3} = u - 15a$ ------------------ Equation $(2)$
Now subtracting the equation $(2)$ from $(1)$ we can deduce
$25 - \dfrac{{50}}{3} = u - u - 5a + 15a$
On further solving the equation we get,
$\dfrac{{25}}{3} = 10a$
$\Rightarrow a = \dfrac{{25}}{{30}}m/{s^2}$
Now substituting the value of $a$ in equation $(2)$ we get
$\dfrac{{50}}{3} = u - 15 \times \dfrac{{25}}{{30}}$
$\Rightarrow \dfrac{{50}}{3} = u - \dfrac{{25}}{2}$
Now rearranging the terms by transpositions we can deduce
$u = \dfrac{{50}}{3} + \dfrac{{25}}{2} = \dfrac{{100 + 75}}{6}$
$\Rightarrow u = \dfrac{{175}}{6}m/s$ ----------------------- Equation $(3)$
Now as we know that the motorcyclist is decelerating and after some time he will come to rest. Let us consider the travels some distance $d$ before coming to rest and its final velocity will become $v = 0m/s$. Hence
$2ad = {v^2} - {u^2}$
$\Rightarrow - 2 \times \dfrac{{25}}{{30}} \times d = {0^2} - {\dfrac{{175}}{{{6^2}}}^2}$
Now solving this equation we get
$d = \dfrac{{175 \times 175 \times 15}}{{36 \times 25}} = \dfrac{{18375}}{{36}}$
$\therefore d = 510.4166m$
As $500m$ is already covered, hence the distance covered by the motorcyclist before coming to rest
$x = 510.4166m - 500m$
$\Rightarrow x = 10.4166m$

So the distance covered by motorcyclists before coming to rest will be $x = 10.4166m$.

Note When we are dealing with such types of problems we have to stay aware of the equations of motion. Also while solving the numerical ensure each physical quantity is in its SI units. If not then proceed with converting it first.